某电视台连续播放6个广告.三个不同的商业广告.三个不同的奥运宣传广告.要求最后播放的不能是商业广告.且奥运宣传广告两两不能连续播放.则不同的播放方式有( ) A.48种B.98种C.108种D.120种题目和参考答案——青夏教育精英家教网—

题目内容

某电视台连续播放6个广告，三个不同的商业广告，三个不同的奥运宣传广告，要求最后播放的不能是商业广告，且奥运宣传广告两两不能连续播放，则不同的播放方式有（　　）

A、48种	B、98种
C、108种	D、120种

考点：排列、组合及简单计数问题

专题：应用题,排列组合

分析：首先排列3个商业广告，有A₃³种结果，再在三个商业广告形成的四个空中排列三个元素，注意最后一个位置一定要有广告共有C₃¹A₃²种结果，根据乘法原理得到结果．

解答： 解：由题意知，这里是元素不相邻的问题，
首先排列3个商业广告，有A₃³=6种结果，
再在三个商业广告形成的四个空中排列三个元素，注意最后一个位置一定要有广告
共有C₃¹A₃²=18种结果，
根据分步计数原理知共有6×18=108种结果，
故选：C

点评：本题考查分步计数原理，注意题目中对于元素要不同的限制条件，一是有不相邻，二是有一个位置不能是一种元素，并且还不能空着，注意这几种不同要求要同时满足．

练习册系列答案

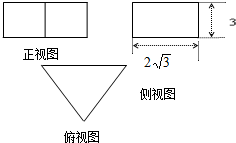一个几何体的底面是正三角形，侧棱垂直于底面，它的三视图及其尺寸如下（单位cm），则该几何体的表面积为（　　）

cm²

cm²

如图所示，等边△ABC的边长为2，D为AC中点，且△ADE也是等边三角形，将△ADE绕看A点顺时针转到到AD与AB重合的过程中，

已知函数f（x）是定义在R上的奇函数，当x＜0时，f（x）=-aln（-x）-（a+1）x．
（1）求f（x）在R上的解析式；
（2）当a＞-1时，讨论f（x）在（0，+∞）上的单调性，并指出其单调区间；
（3）若对于任意的x∈（0，+∞），f（x）≥-

x2恒成立，求实数a的取值范围．

为了了解某种产品的质量，抽取容量为30的样本，检测结果为一级品5件，二级品8件．三级品13件，其余的部是次品．已知样本频率分布表的一部分如图所示：

产品	频数	频率
一级品	5	0.17
二级品	8
三级品	13	0.43
次品		0.13

（1）请将样本频率分布表补充完整，并画出样本频率分布条形图；
（2）任意抽取一件产品，试估计它是一级品或二级品的概率为多少？

直角坐标系下的（1，1）化成极坐标系下的坐标为

．

从某校随机抽取100名学生，获得了他们一周课外阅读时间（单位：小时）的数据，整理得到数据分组及频数分步和频率分布直方图

组号	分组	频数
1	[0，2）	6
2	[2，4）	8
3	[4，6）	17
4	[6，8）	22
5	[8，10）	25
6	[10，12）	12
7	[12，14）	6
8	[14，16）	2
9	[16，18）	2
合计	100

（Ⅰ）从该校随机选取一名学生，试估计这名学生该周课外阅读时间少于12小时的频率；
（Ⅱ）求频率分布直方图中的a，b的值．

关于直线m、n与平面α、β，有下列四个命题：
①m∥α，n∥β且α∥β，则m∥n；
②m⊥α，n⊥β且α⊥β，则m⊥n；
③m⊥α，n∥β且α∥β，则m⊥n；
④m∥α，n⊥β且α⊥β，则m∥n．
其中正确命题的个数是（　　）

试题分类