Question

如图所示，等边△ABC的边长为2，D为AC中点，且△ADE也是等边三角形，将△ADE绕看A点顺时针转到到AD与AB重合的过程中，

BD

•

CE

的最大值是（　　）

• A、

  3

  2

• B、

  3 2

  2

• C、

  3 3

  2

• D、

  9

  2

Answer 1

考点：平面向量数量积的运算

专题：计算题,三角函数的图像与性质,平面向量及应用

分析：设∠BAD=θ，（0≤θ≤

π

3

），则∠CAE=θ，则

BD

•

CE

=（

AD

-

AB

）•（

AE

-

AC

）将其展开，运用向量的数量积的定义，再由两角和差的余弦公式，化简得到

5

2

-2cosθ，再由余弦函数的性质，即可得到范围．

解答： 解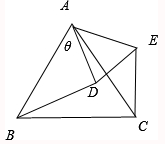：设∠BAD=θ，（0≤θ≤

π

3

），
则∠CAE=θ，
则

BD

•

CE

=（

AD

-

AB

）•（

AE

-

AC

）
=

AD

•

AE

-

AD

•

AC

-

AB

•

AE

+

AB

•

AC

=1×1×cos

π

3

-1×2×cos（

π

3

-θ）-2×1×cos（

π

3

+θ）+2×2×cos

π

3

=

5

2

-2（

1

2

cosθ+

3

2

sinθ+

1

2

cosθ-

3

2

sinθ）=

5

2

-2cosθ，
由于0≤θ≤

π

3

，则

1

2

≤cosθ≤1，
则

1

2

≤

5

2

-2cosθ≤

3

2

．
故选A．

点评：本题考查平面向量的数量积的定义，考查三角函数的化简和求最值，考查运算能力，属于中档题．