题目内容
10.已知p:4x2+12x-7≤0,q:a-3≤x≤a+3.(1)当a=0时,若p真q假,求实数x的取值范围;
(2)若p是q的充分条件,求实数a的取值范围.
分析 (1)将a=0代入q,求出x的范围即可;(2)根据集合的包含关系得到关于a的不等式组,解出即可.
解答 解:由4x2+12x-7≤0,解得:-$\frac{7}{2}$≤x≤$\frac{1}{2}$,q:a-3≤x≤a+3.
(1)当a=0时,q:-3≤x≤3,
若p真q假,则-$\frac{7}{2}$≤x<-3;
(2)若p是q的充分条件,
则$\left\{\begin{array}{l}{-\frac{7}{2}≥a-3}\\{\frac{1}{2}≤a+3}\end{array}\right.$,
解得:-$\frac{5}{2}$≤x≤-$\frac{1}{2}$,
点评 本题考察了复合命题的判断,考察充分必要条件,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知某圆锥曲线C的极坐标方程是ρ2=$\frac{225}{9+16co{s}^{2}θ}$,则曲线C的离心率为( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{4}$ |
19.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的两个焦点分别为F1,F2,|F1F2|=2c(c>0).若点P在椭圆上,且∠F1PF2=90°,则点P到x轴的距离为( )
| A. | $\frac{b^2}{a}$ | B. | $\frac{b^2}{c}$ | C. | $\frac{c^2}{a}$ | D. | $\frac{c^2}{b}$ |
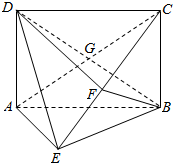 如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.
如图,四边形ABCD是矩形,DA⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC和BD交于点G.