题目内容
已知函数f(x)=
,则不等式1<f(x)<4的解集为 .
|
考点:其他不等式的解法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:由已知可得,不等式1<f(x)<4即为
或
,运用指数函数的单调性和二次不等式的解法,分别解出它们,再求并集即可.
|
|
解答:
解:由已知可得,不等式1<f(x)<4
即为
或
即
或
,
解得,0<x≤1或3<x<4.
则解集为(0,1]∪(3,4).
故答案为:(0,1]∪(3,4).
即为
|
|
即
|
|
解得,0<x≤1或3<x<4.
则解集为(0,1]∪(3,4).
故答案为:(0,1]∪(3,4).
点评:本题考查分段函数的运用:解不等式,考查指数函数的单调性,及二次不等式的解法,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
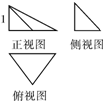 一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积是( )
一个几何体的三视图如图所示,其中俯视图是一个腰长为2的等腰直角三角形,则该几何体外接球的体积是( )| A、36π | ||
| B、9π | ||
C、
| ||
D、
|
已知定义在R上的单调函数f(x)满足:存在实数x0,使得对于任意实数x1,x2,总有f(x0x1+x0x2)=f(x0)+f(x1)+f(x2)恒成立.求:
(1)f(1)+f(0);
(2)x0的值.
(1)f(1)+f(0);
(2)x0的值.
若点(2,k)到直线5x-12y+6=0的距离是4,则k的值是( )
| A、1 | ||
| B、-3 | ||
C、1或
| ||
D、-3或
|
在△ABC中,角A,B,C所对的边分别为a,b,c,S表示△ABC的面积,若acosB+bcosA=csinC,S=
(b2+c2-a2),则∠B=( )
| 1 |
| 4 |
| A、90° | B、60° |
| C、45° | D、30° |
已知全集U={x|
>0,x∈N*},集合A={2,3},则∁UA=( )
| x-1 |
| 5-x |
| A、{2,3,4} |
| B、{2,3} |
| C、{4} |
| D、{1,4} |
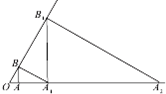 如图,在△OAB中,OA⊥AB,OB=1,OA=
如图,在△OAB中,OA⊥AB,OB=1,OA=