题目内容
1.已知i为虚数单位,a∈R,若(a2+2a-3)+(a+3)i为纯虚数,则a的值为( )| A. | 1 | B. | -3 | C. | -3或1 | D. | 3或1 |
分析 直接由实部等于0且虚部不为0列式求得a值.
解答 解:∵(a2+2a-3)+(a+3)i为纯虚数,
∴$\left\{\begin{array}{l}{{a}^{2}+2a-3=0}\\{a+3≠0}\end{array}\right.$,解得:a=1.
故选:A.
点评 本题考查复数的基本概念,考查复数是纯虚数的条件,是基础题.

练习册系列答案
相关题目
11.已知双曲线C的渐近线方程为3x±2y=0,且经过点$(4,3\sqrt{2})$,则该双曲线的方程为( )
| A. | $\frac{x^2}{8}-\frac{y^2}{9}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{16}=1$ | C. | $\frac{x^2}{8}-\frac{y^2}{18}=1$ | D. | $\frac{y^2}{18}-\frac{x^2}{16}=1$ |
12.有一个容量为66的样本,数据的分组及各组的数据如下:估计数据落在[31.5,43.5]的概率是( )
| 分组 | [11.5,15.5) | [15.5,19.5) | [19.5,23.5) | [23.5,27.5) |
| 频数 | 2 | 4 | 9 | 18 |
| 分组 | [27.5,31.5) | [31.5,35.5) | [35.5,39.5) | [39.5,43.5) |
| 频数 | 11 | 12 | 7 | 3 |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
6.设公差不为零的等差数列{an}的前n项和为Sn,若a4=2(a2+a3),则$\frac{S_7}{S_4}$=( )
| A. | $\frac{7}{4}$ | B. | $\frac{14}{5}$ | C. | 7 | D. | 14 |
10.将4名大学生分配到A,B,C三个不同的学校实习,每个学校至少分配一人,若甲要求不到A学校,则不同的分配方案共有( )
| A. | 36种 | B. | 30种 | C. | 24种 | D. | 20种 |
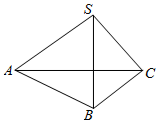 如图,在四面体S-ABC中,SA、SB、SC两两垂直,∠SBA=45°,∠SBC=60°,求:
如图,在四面体S-ABC中,SA、SB、SC两两垂直,∠SBA=45°,∠SBC=60°,求: