题目内容
2.要计算$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2016}$的结果,下面的程序框图中的横线上可以填( )
| A. | n<2016? | B. | n≤2016? | C. | n>2016? | D. | n≥2016? |
分析 通过观察程序框图,分析为填判断框内判断条件,n的值在执行运算之后还需加1,故判断框内数字应减1,按照题意填入判断框即可.
解答 解:通过分析,本程序框图为“当型“循环结构,
判断框内为满足循环的条件,
第1次循环,S=1,n=1+1=2,
第2次循环,S=1+$\frac{1}{2}$,n=2+1=3,
…
当n=2017时,由题意,此时,应该不满足条件,退出循环,输出S的值.
所以,判断框内的条件应为:n≤2016.
故选:B.
点评 本题考查程序框图,通过对程序框图的分析对判断框进行判断,属于基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
10.已知椭圆和双曲线焦点F1,F2相同,且离心率互为倒数,P是椭圆和双曲线在第一象限的交点,当∠F1PF2=60°时,椭圆的离心率为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
14.执行如图所示的程序框图,如果输出的k的值为3,则输入的a的值可以是( )
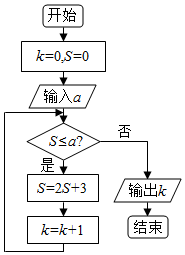

| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
11.已知双曲线C的渐近线方程为3x±2y=0,且经过点$(4,3\sqrt{2})$,则该双曲线的方程为( )
| A. | $\frac{x^2}{8}-\frac{y^2}{9}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{16}=1$ | C. | $\frac{x^2}{8}-\frac{y^2}{18}=1$ | D. | $\frac{y^2}{18}-\frac{x^2}{16}=1$ |
12.有一个容量为66的样本,数据的分组及各组的数据如下:估计数据落在[31.5,43.5]的概率是( )
| 分组 | [11.5,15.5) | [15.5,19.5) | [19.5,23.5) | [23.5,27.5) |
| 频数 | 2 | 4 | 9 | 18 |
| 分组 | [27.5,31.5) | [31.5,35.5) | [35.5,39.5) | [39.5,43.5) |
| 频数 | 11 | 12 | 7 | 3 |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 在三棱柱PBC-QAD中,侧面ABCD为矩形,PA⊥CD.
在三棱柱PBC-QAD中,侧面ABCD为矩形,PA⊥CD.