题目内容
19.下列说法错误的是( )| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” | |
| B. | 对于命题p:?x0∈R,x${\;}_{0}^{2}$+x0+1<0,则¬p:?x∈R,x2+x+1≥0 | |
| C. | 若m,n∈R,“lnm<lnn”是“em<en”的充分不必要条件 | |
| D. | 若p∧q为假命题,则p、q均为假命题 |
分析 A利用逆否命题的定义判断即可;
B存在命题,应把存在改为任意,再否定结论;
C根据充分不必要条件的定义判断即可;
D根据且命题的真假判断依据判断即可.
解答 解:对于A,逆否命题把命题的条件和结论互换,再同时否定,故命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”,故正确;
对于B,对于存在命题,应把存在改为任意,再否定结论,故命题p:?x0∈R,x${\;}_{0}^{2}$+x0+1<0,则¬p:?x∈R,x2+x+1≥0,故正确;
对于C,若m,n∈R,“lnm<lnn”,则0<m<n,可得“em<en”,但由“em<en”,m,n也可能为负值,不一定得出lnm<lnn”,故应是充分不必要条件,故正确;
对于D,且命题为假命题,p和q不能都是真命题,但也不一定都是假命题,故错误.
故选:D.
点评 考查了四中命题间的逻辑关系,属于常规题型,应熟练掌握.

练习册系列答案
相关题目
10.已知椭圆和双曲线焦点F1,F2相同,且离心率互为倒数,P是椭圆和双曲线在第一象限的交点,当∠F1PF2=60°时,椭圆的离心率为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
14.执行如图所示的程序框图,如果输出的k的值为3,则输入的a的值可以是( )
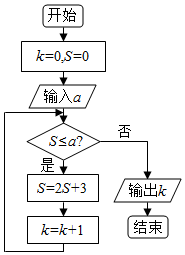

| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
11.已知双曲线C的渐近线方程为3x±2y=0,且经过点$(4,3\sqrt{2})$,则该双曲线的方程为( )
| A. | $\frac{x^2}{8}-\frac{y^2}{9}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{16}=1$ | C. | $\frac{x^2}{8}-\frac{y^2}{18}=1$ | D. | $\frac{y^2}{18}-\frac{x^2}{16}=1$ |
8.已知数1、a、b成等差数列,而1、b、a成等比数列,若a≠b,则a的值为( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
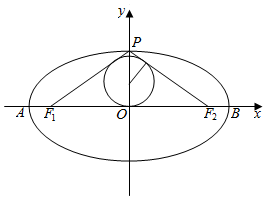 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点的坐标分别为A(-2,0),B(2,0),离心率$e=\frac{{\sqrt{3}}}{2}$
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点的坐标分别为A(-2,0),B(2,0),离心率$e=\frac{{\sqrt{3}}}{2}$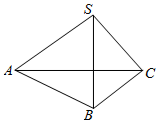 如图,在四面体S-ABC中,SA、SB、SC两两垂直,∠SBA=45°,∠SBC=60°,求:
如图,在四面体S-ABC中,SA、SB、SC两两垂直,∠SBA=45°,∠SBC=60°,求: