题目内容
20.已知椭圆Γ的中心在坐标原点,且经过点$(1,\frac{3}{2})$,它的一个焦点与抛物线E:y2=4x的焦点重合,斜率为k的直线l交抛物线E于A、B两点,交椭圆Γ于C、D两点.(1)求椭圆Γ的方程;
(2)直线l经过点F(1,0),设点P(-1,k),且△PAB的面积为$4\sqrt{3}$,求k的值;
(3)若直线l过点M(0,-1),设直线OC,OD的斜率分别为k1,k2,且$\frac{1}{k_1},\frac{2}{k},\frac{1}{k_2}$成等差数列,求直线l的方程.
分析 (1)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由椭圆Γ的中心在坐标原点,且经过点$(1,\frac{3}{2})$,它的一个焦点与抛物线E:y2=4x的焦点重合,列出方程组求出a,b,由此能求出椭圆Γ的方程.
(2)设直线l:y=k(x-1),由$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,得k2x2-2(k2+2)x+k2=0,由此利用根的判别式、韦达定理、弦长公式、点到直线距离公式,结合已知条件能求出k的值.
(3)设直线l:y=kx-1,代入椭圆,得(4k2+3)x2-8kx-8=0,由此利用M(0,-1)在椭圆内部,得l与椭圆恒有两个交点,根据韦达定理、等差数列的性质,结合已知条件能求出直线l的方程.
解答 解:(1)设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题设$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{9}{4{b}^{2}}=1}\\{{a}^{2}={b}^{2}+1}\end{array}\right.$,
解得a2=4,b2=3,
∴椭圆Γ的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)设直线l:y=k(x-1),
由$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,得k2x2-2(k2+2)x+k2=0,
l与抛物线E有两个交点,k≠0,
△=16(k2+1)>0,
则|AB|=$\frac{\sqrt{4({k}^{4}+4{k}^{2}+4)-4{k}^{4}}}{{k}^{2}}$•$\sqrt{1+{k}^{2}}$=$\frac{4({k}^{2}+1)}{{k}^{2}}$,
P(-1,k)到l的距离d=$\frac{3|k|}{\sqrt{{k}^{2}+1}}$,
又${S}_{△PAB}=4\sqrt{3}$,
∴$\frac{1}{2}×\frac{4({k}^{2}+1)}{{k}^{2}}$•$\frac{3|k|}{\sqrt{{k}^{2}+1}}$=4$\sqrt{3}$,即4k2=3k2+3,
解得k=$±\sqrt{3}$.
(3)设直线l:y=kx-1,由$\left\{\begin{array}{l}{y=kx-1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得(4k2+3)x2-8kx-8=0,M(0,-1)在椭圆内部,
∴l与椭圆恒有两个交点,
设C(x1,y1),D(x2,y2),则${x}_{1}+{x}_{2}=\frac{8k}{4{k}^{2}+3}$,${x}_{1}{x}_{2}=-\frac{8}{4{k}^{2}+3}$,
由$\frac{1}{k_1},\frac{2}{k},\frac{1}{k_2}$成等差数列,
得$\frac{4}{k}$=$\frac{1}{{k}_{1}}+\frac{1}{{k}_{2}}$=$\frac{{x}_{1}}{{y}_{1}}+\frac{{x}_{2}}{{y}_{2}}$=$\frac{{x}_{1}{y}_{2}+{x}_{2}{y}_{1}}{{y}_{1}{y}_{2}}$=$\frac{{x}_{1}(k{x}_{2}-1)+{x}_{2}(k{x}_{1}-1)}{{y}_{1}{y}_{2}}$
=$\frac{2k{x}_{1}{x}_{2}-({x}_{1}+{x}_{2})}{{k}^{2}{x}_{1}{x}_{2}-k({x}_{1}+{x}_{2})+1}$=$\frac{-16k-8k}{-8{k}^{2}-8{k}^{2}+4{k}^{2}+3}$=$\frac{24k}{12{k}^{2}-3}$,
解得k=$±\frac{\sqrt{2}}{2}$,
∴直线l的方程为y=$±\frac{\sqrt{2}}{2}x-1$.
点评 本题考查椭圆方程、直线斜率、直线方程的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、弦长公式、点到直线距离公式,等差数列等知识点的合理运用.

| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{x^2}{8}-\frac{y^2}{9}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{16}=1$ | C. | $\frac{x^2}{8}-\frac{y^2}{18}=1$ | D. | $\frac{y^2}{18}-\frac{x^2}{16}=1$ |
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
| A. | -200 | B. | -160 | C. | -120 | D. | -40 |
| 分组 | [11.5,15.5) | [15.5,19.5) | [19.5,23.5) | [23.5,27.5) |
| 频数 | 2 | 4 | 9 | 18 |
| 分组 | [27.5,31.5) | [31.5,35.5) | [35.5,39.5) | [39.5,43.5) |
| 频数 | 11 | 12 | 7 | 3 |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
| A. | 36种 | B. | 30种 | C. | 24种 | D. | 20种 |
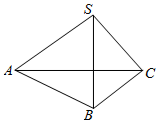 如图,在四面体S-ABC中,SA、SB、SC两两垂直,∠SBA=45°,∠SBC=60°,求:
如图,在四面体S-ABC中,SA、SB、SC两两垂直,∠SBA=45°,∠SBC=60°,求: