题目内容
16.函数f(x)的部分图象如图所示,则f(x)的解析式可以是( )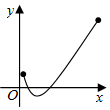
| A. | f(x)=2x+lgx+2 | B. | f(x)=2x+lgx-2 | C. | f(x)=2x-lgx+2 | D. | f(x)=2x-lgx-2 |
分析 根据函数的单调性排除A,B,根据函数的零点存在定理,排除C,肯定D.
解答 解:对于A,B函数均为单调增函数,故不符合,
对于C:f(x)=2x-lgx+2,令f(x)=0,得到y=2x+2,与y=lgx,则其图象没有交点,即没有零点,故C不符合,
对于D:f(x)=2x-lgx-2,令f(x)=0,得到y=2x-2,与y=lgx,则其图象有两个交点,故D符合,
故选:D.
点评 本题考查了函数图象的识别,关键是掌握函数的单调性和基本函数图象的画法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知双曲线C的渐近线方程为3x±2y=0,且经过点$(4,3\sqrt{2})$,则该双曲线的方程为( )
| A. | $\frac{x^2}{8}-\frac{y^2}{9}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{16}=1$ | C. | $\frac{x^2}{8}-\frac{y^2}{18}=1$ | D. | $\frac{y^2}{18}-\frac{x^2}{16}=1$ |
8.已知数1、a、b成等差数列,而1、b、a成等比数列,若a≠b,则a的值为( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
6.设公差不为零的等差数列{an}的前n项和为Sn,若a4=2(a2+a3),则$\frac{S_7}{S_4}$=( )
| A. | $\frac{7}{4}$ | B. | $\frac{14}{5}$ | C. | 7 | D. | 14 |
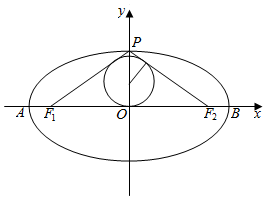 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点的坐标分别为A(-2,0),B(2,0),离心率$e=\frac{{\sqrt{3}}}{2}$
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点的坐标分别为A(-2,0),B(2,0),离心率$e=\frac{{\sqrt{3}}}{2}$