题目内容
已知椭圆E：
+
=1，点P（x，y）是椭圆上一点．求x2+y2的最值．
| x2 |
| 25 |
| y2 |
| 16 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设P（5cosα，4sinα），则x2+y2=25cos2α+16sin2α=25-9sin2α，从而可求x2+y2的最值．
解答：
解：设P（5cosα，4sinα），则x2+y2=25cos2α+16sin2α=25-9sin2α，
∴sinα=0时，x2+y2取得最大值25，sinα=±1时，x2+y2取得最大值16．
∴sinα=0时，x2+y2取得最大值25，sinα=±1时，x2+y2取得最大值16．
点评：本题考查椭圆的方程，考查参数法的运用，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
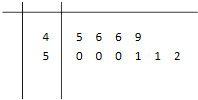一批食品，每袋的标准重量是50g，为了了解这批食品的实际重量情况，从中随机抽取10袋食品，称出各袋的重量（单位：g），并得到其茎叶图（如图）．