题目内容
在某贫困山区活跃着一支大学生志愿服务队,在2014年暑假期间,他们参加活动的有关数据统计如下:
(1)从志愿服务队中任选2人,求这2人参加活动次数不相同的概率;
(2)从志愿服务队中任选3人,求这3人中仅有2人活动次数相同的概率.
| 参加活动人数 | 1 | 2 |
| 人数 | 2 | 3 |
(2)从志愿服务队中任选3人,求这3人中仅有2人活动次数相同的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)从志愿服务队中任选2人,共有C52=10种,这2人参加活动次数不相同的选法有C21C31=6.根据概率公式计算即可,
(2)从志愿服务队中任选3人,共有C53=10种,这3人中仅有2人活动次数相同,有C22C31+C21C32=9,根据概率公式计算即可.
(2)从志愿服务队中任选3人,共有C53=10种,这3人中仅有2人活动次数相同,有C22C31+C21C32=9,根据概率公式计算即可.
解答:
解:(1)从志愿服务队中任选2人,共有C52=10种,这2人参加活动次数不相同的选法有C21C31=6.
故这2人参加活动次数不相同的概率P=
=
(2)从志愿服务队中任选3人,共有C53=10种,这3人中仅有2人活动次数相同,有C22C31+C21C32=9
故3人中仅有2人活动次数相同的概率P=
故这2人参加活动次数不相同的概率P=
| 6 |
| 10 |
| 3 |
| 5 |
(2)从志愿服务队中任选3人,共有C53=10种,这3人中仅有2人活动次数相同,有C22C31+C21C32=9
故3人中仅有2人活动次数相同的概率P=
| 9 |
| 10 |
点评:本题考查等可能事件的概率以及利用概率知识解决实际问题的能力,属于基础题

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
若向量
=(0,1),
=(2,-1),
=(1,1),则( )
| a |
| b |
| c |
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、|
|
在空间直角坐标系O-xyz中,一个四面体的顶点坐标为分别为(0,0,2),(2,2,0),(0,2,0),(2,2,2).画该四面体三视图中的正视图时,以xOz平面为投影面,则得到正视图可以为( )
A、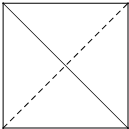 |
B、 |
C、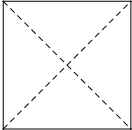 |
D、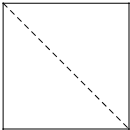 |
过点P(3,1)作圆C:(x-2)2+y2=1的两条切线,切点分别为A、B,则直线AB的方程为( )
| A、x+y-3=0 |
| B、x-y-3=0 |
| C、2x-y-3=0 |
| D、2x+y-3=0 |
已知线段PQ的两个端点的坐标分别为P(-1,6)、Q(2,2),若直线mx+y-m=0与线段PQ有交点,则实数m的取值范围是( )
| A、(-∞,-2]∪[3,+∞) |
| B、(-∞,-3]∪[2,+∞) |
| C、[-2,3] |
| D、[-3,2] |
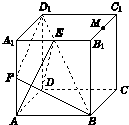 如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱A1B1、AA1、B1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱A1B1、AA1、B1C1的中点.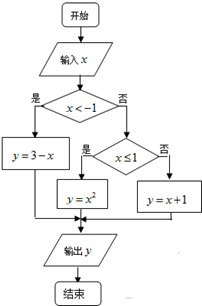 阅读右边的算法流程图(如图),解答下列问题:
阅读右边的算法流程图(如图),解答下列问题: