题目内容
直线
x-3y+5=0的倾斜角为( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
考点:直线的倾斜角
专题:直线与圆
分析:求出直线的斜率,根据倾斜角和斜率之间的关系即可得到结论.
解答:
解:直线斜截式方程为y=
x+
,
即直线的斜率k=
,
∵tan30°=
,
∴直线的倾斜角为30°,
故选:A
| ||
| 3 |
| 5 |
| 3 |
即直线的斜率k=
| ||
| 3 |
∵tan30°=
| ||
| 3 |
∴直线的倾斜角为30°,
故选:A
点评:本题考查直线的倾斜角和直线的斜率之间的关系,本题解题的关键是知道两者之间的关系,比较基础.

练习册系列答案
相关题目
已知f(x)=
是(-∞,+∞)上的增函数,那么实数a的取值范围是( )
|
| A、(0,3) | ||
| B、(1,3) | ||
| C、(1,+∞) | ||
D、[
|
已知线段PQ的两个端点的坐标分别为P(-1,6)、Q(2,2),若直线mx+y-m=0与线段PQ有交点,则实数m的取值范围是( )
| A、(-∞,-2]∪[3,+∞) |
| B、(-∞,-3]∪[2,+∞) |
| C、[-2,3] |
| D、[-3,2] |
已知等比数列{an}的各项均为正数,且a2,
a3,2a1成等差数列,则该数列的公比为( )
| 1 |
| 2 |
A、1+
| ||
B、1±
| ||
| C、-1 | ||
| D、1 |
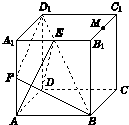 如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱A1B1、AA1、B1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱A1B1、AA1、B1C1的中点.