题目内容
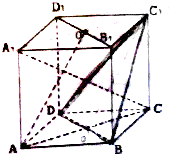 如图,在正方体ABCD-A1B1C1D1中,O是面对角线B1D1的中点.
如图,在正方体ABCD-A1B1C1D1中,O是面对角线B1D1的中点.(1)求证:AO∥平面BDC1;
(2)求证:A1C⊥平面BDC1.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)如图所示,连接AC,BD交于G点,连接OC1,GC1,由OC1
AG,可得OA∥GC1,从而可证OA∥平面C1BD.
(2)连接AC,交BD于O,则BD⊥AC,结合A1A⊥BD,由线面垂直的判定定理得BD⊥平面A1AC,进而BD⊥A1C,连接C1O,可证得A1C⊥C1O,再利用线面垂直的判定定理即可得到A1C⊥平面C1BD;
| ∥ |
. |
(2)连接AC,交BD于O,则BD⊥AC,结合A1A⊥BD,由线面垂直的判定定理得BD⊥平面A1AC,进而BD⊥A1C,连接C1O,可证得A1C⊥C1O,再利用线面垂直的判定定理即可得到A1C⊥平面C1BD;
解答:
证明:(1)如图所示,连接AC,BD交于G点,连接OC1,GC1,
∴在正方体ABCD-A1B1C1D1中,OC1
AG,四边形OC1AG为平行四边形,
∴OA∥GC1,
又GC1?平面C1BD,OA?平面C1BD,∴OA∥平面C1BD.…(2分)
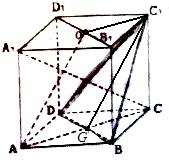
(2)连接AC,交BD于O,则BD⊥AC.
又A1A⊥BD,∴BD⊥平面A1AC.
∵A1C?平面A1AC,BD⊥A1C.
连接C1O,在矩形A1C1CA中,设A1C交C1O于M.
由
=
,知∠ACA1=∠CC1O.
∴∠C1OC+A1CO=∠C1OC+∠CC1O=
,∴∠CMO=
,
∴A1C⊥C1O.
又CO∩BD=0,CO?平面C1BD,BD?平面C1BD,
∴A1C⊥平面C1BD.…(7分)
∴在正方体ABCD-A1B1C1D1中,OC1
| ∥ |
. |
∴OA∥GC1,
又GC1?平面C1BD,OA?平面C1BD,∴OA∥平面C1BD.…(2分)

(2)连接AC,交BD于O,则BD⊥AC.
又A1A⊥BD,∴BD⊥平面A1AC.
∵A1C?平面A1AC,BD⊥A1C.
连接C1O,在矩形A1C1CA中,设A1C交C1O于M.
由
| A1A |
| AC |
| OC |
| CC1 |
∴∠C1OC+A1CO=∠C1OC+∠CC1O=
| π |
| 2 |
| π |
| 2 |
∴A1C⊥C1O.
又CO∩BD=0,CO?平面C1BD,BD?平面C1BD,
∴A1C⊥平面C1BD.…(7分)
点评:直线与平面平行的判定,直线与平面垂直的判定,解题时要认真审题,注意空间思维能力的培养,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在空间直角坐标系O-xyz中,一个四面体的顶点坐标为分别为(0,0,2),(2,2,0),(0,2,0),(2,2,2).画该四面体三视图中的正视图时,以xOz平面为投影面,则得到正视图可以为( )
A、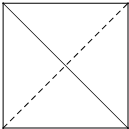 |
B、 |
C、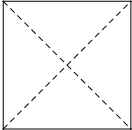 |
D、 |
过点P(3,1)作圆C:(x-2)2+y2=1的两条切线,切点分别为A、B,则直线AB的方程为( )
| A、x+y-3=0 |
| B、x-y-3=0 |
| C、2x-y-3=0 |
| D、2x+y-3=0 |
已知f(x)=
是(-∞,+∞)上的增函数,那么实数a的取值范围是( )
|
| A、(0,3) | ||
| B、(1,3) | ||
| C、(1,+∞) | ||
D、[
|
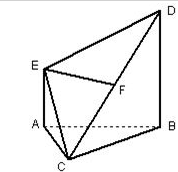 如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,△ABC是边长为2的正三角形,且BD=2,AE=1,F为CD中点.
如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,△ABC是边长为2的正三角形,且BD=2,AE=1,F为CD中点.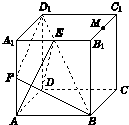 如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱A1B1、AA1、B1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱A1B1、AA1、B1C1的中点.