题目内容
已知双曲线
-
=1(a>0,b>0)与圆 x2+y2=c2(c=
)交于A,B,C,D四点,若四边形ABCD是正方形,则双曲线的离心率是 .
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:联立双曲线方程和圆方程,求得交点,由于四边形ABCD是正方形,则有x2=y2,即为c2-
=
,运用双曲线的a,b,c的关系和离心率公式,即可得到结论.
| b4 |
| c2 |
| b4 |
| c2 |
解答:
解:联立双曲线方程
-
=1和圆x2+y2=c2,
解得,x2=c2-
,y2=
,
由于四边形ABCD是正方形,
则有x2=y2,即为c2-
=
,
即c4=2b4,即c2=
b2=
(c2-a2),
则e=
=
=
.
故答案为:
.
| x2 |
| a2 |
| y2 |
| b2 |
解得,x2=c2-
| b4 |
| c2 |
| b4 |
| c2 |
由于四边形ABCD是正方形,
则有x2=y2,即为c2-
| b4 |
| c2 |
| b4 |
| c2 |
即c4=2b4,即c2=
| 2 |
| 2 |
则e=
| c |
| a |
|
|
故答案为:
|
点评:本题考查双曲线方程和性质,考查联立双曲线方程和圆的方程求解交点,考查离心率的求法,属于基础题.

练习册系列答案
相关题目
函数f(x)的图象如图所示,则不等式(x+3)•f′(x)<0的解集为( )


| A、(l,+∞) |
| B、(-∞,-3) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-∞,-3)∪(-1,1) |
过点P(3,1)作圆C:(x-2)2+y2=1的两条切线,切点分别为A、B,则直线AB的方程为( )
| A、x+y-3=0 |
| B、x-y-3=0 |
| C、2x-y-3=0 |
| D、2x+y-3=0 |
曲线y=
+1(-2≤x≤2)与直线y=kx-2k+4有两个不同的交点时实数k的范围是( )
| 4-x2 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-∞,
|
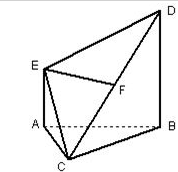 如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,△ABC是边长为2的正三角形,且BD=2,AE=1,F为CD中点.
如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,△ABC是边长为2的正三角形,且BD=2,AE=1,F为CD中点.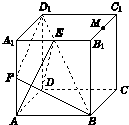 如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱A1B1、AA1、B1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱A1B1、AA1、B1C1的中点.