题目内容
n∈N*，则（20-n）（21-n）…（100-n）等于（ ）
A、A
| ||
B、A
| ||
C、A
| ||
D、A
|
考点：二项式系数的性质
专题：二项式定理
分析：由条件利用排列数公式，可得结论．
解答：
解：由于（20-n）（21-n）…（100-n）表示81个连续自然数的乘积，
最大的项是100-n，最小的项为 20-n，
根据排列数公式可得它可用A
表示，
故选：C．
最大的项是100-n，最小的项为 20-n，
根据排列数公式可得它可用A
81 100-n |
故选：C．
点评：本题主要考查排列数公式的应用，属于基础题．
练习册系列答案
高中必刷题系列答案
相关题目
函数y=
x2+
（x＞0）的最小值为（ ）
| 3 |
| 16 |
| 3 |
| x |
A、
| |||||
B、
| |||||
| C、不存在 | |||||
| D、1 |
已知幂函数y=f（x）的图象经过点（16，4），则f（
）的值为（ ）
| 1 |
| 64 |
| A、3 | ||
B、
| ||
C、
| ||
D、
|
设命题p和命题q，“p∨q”的否定是真命题，则必有（ ）
| A、p真q真 | B、p假q假 |
| C、p真q假 | D、p假q真 |
语句“若a＞b，则a2＞b2”（ ）
| A、不是命题 | B、假命题 |
| C、是真命题 | D、不能判定真假 |
已知奇函数f（x）在[-1，0]上为单调递减函数，又α、β为锐角三角形两内角且α＞β，则下列结论正确的是（ ）
| A、f（cos α）＞f（cos β） |
| B、f（sin α）＞f（sin β） |
| C、f（sin α）＞f（cos β） |
| D、f（sin α）＜f（cos β） |
集训队有6男4女共10名运动员，其中男女队长各1人，现选派5人外出参赛，则队长中至少有1人参加的选派方法共有（ ）
| A、140种 | B、126种 |
| C、196种 | D、192种 |
现有五名实习大学生分到四个班实习，每班至少分配一名，则不同分法的种数为（ ）
| A、45 | ||||
B、A
| ||||
C、C
| ||||
D、C
|
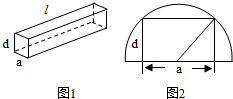如图1所示，一根水平放置的长方体枕木的安全负荷与它的宽度a成正比，与它的厚度d的平方成正比，与它的长度l的平方成反比．