题目内容
已知数列{an}中,a1=1,an+1=2an-3,则数列{an}的通项公式为( )
A、an=
| |||||
| B、an=3+(-2)n | |||||
| C、an=3-2n | |||||
| D、an=-3+2n+1 |
考点:数列递推式
专题:等差数列与等比数列
分析:由已知条件推导出an+1-3=2(an-3),a1-3=-2,从而得到{an-3}是首项为-2,公比为2的等比数列,由此能求出数列{an}的通项公式.
解答:
解:∵数列{an}中,a1=1,an+1=2an-3,
∴an+1-3=2(an-3),a1-3=-2,
∴
=2,
∴{an-3}是首项为-2,公比为2的等比数列,
∴an-3=(-2)•2n-1=-2n,
∴an=3-2n.
故选:C.
∴an+1-3=2(an-3),a1-3=-2,
∴
| an+1-3 |
| an-3 |
∴{an-3}是首项为-2,公比为2的等比数列,
∴an-3=(-2)•2n-1=-2n,
∴an=3-2n.
故选:C.
点评:本题考查数列的通项公式的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
设双曲线
-
=1(a>0)的渐近线方程为3x±2y=0,则a的值为( )
| x2 |
| a2 |
| y2 |
| 9 |
| A、4 | B、3 | C、2 | D、1 |
由直线x=-
,x=-2,曲线y=
及x轴所围图形的面积是( )
| 1 |
| 2 |
| 1 |
| x |
A、
| ||
B、
| ||
C、
| ||
| D、2ln2 |
设?的分布列为
又设y=2?+5 则 Ey=( )
| ? | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=ex(sinx-cosx),若0≤x≤2014π,则函数f(x)的各极大值之和为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=ax3+bx2+cx+d的图象如图所示,则一定有( )
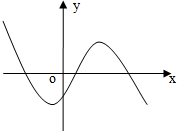
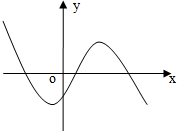
| A、a<0 b>0 c>0 d<0 |
| B、a<0 b<0 c>0 d<0 |
| C、a<0 b>0 c<0 d<0 |
| D、a<0 b<0 c<0 d<0 |
已知x1,x2∈[-
,
],且x1sinx1-x2sinx2<0,则下列结论正确的是( )
| π |
| 2 |
| π |
| 2 |
| A、x13<x23 |
| B、x1+x2<0 |
| C、|x1|>|x2| |
| D、|x1|<|x2| |
设正项等比数列{an}的前n项和为Sn,且210S30+S10=(210+1)S20,则数列{an}的公比为( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=sinx-x,则下列错误的是( )
| A、f(x)为奇函数 |
| B、f(x)在R上单调递减 |
| C、f(x)在R上无极值点 |
| D、f(x)在R上有三个零点 |