题目内容
10.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{2-x},x<2}\\{\frac{3}{4}{x}^{2}-3x+4,x≥2}\end{array}\right.$,若不等式a≤f(x)≤b的解集恰好为[a,b],则b-a=4.分析 通过作出函数y=f(x)的图象,利用a≤2且f(a)=f(b)=b,可知b=4,a=0.
解答 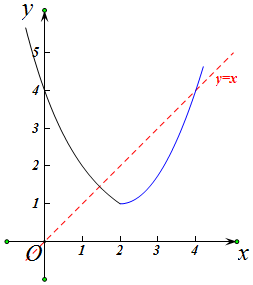 解:因为y=22-x=4×$(\frac{1}{2})^{x}$的图象在R上单调递减,
解:因为y=22-x=4×$(\frac{1}{2})^{x}$的图象在R上单调递减,
且过定点(0,4),
y=$\frac{3}{4}$x2-3x+4的图象是对称轴为x=2,开口向上的抛物线,
所以容易得到函数y=f(x)的图象,如图,
且y=f(x)在(-∞,2)上单调递减,
在(2,+∞)上单调递增,
因为不等式a≤f(x)≤b的解集恰好为[a,b],
所以a≤2,且f(a)=f(b)=b,易知b=4,a=0,
所以b-a=4-0=4,
故答案为:4.
点评 本题是一道关于分段函数的应用题,考查数形结合能力,考查分析问题的能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
1.上饶高铁站B1进站口有3个闸机检票通道口,若某一家庭有3个人检票进站,如果同一个人进的闸机检票通道口选法不同,或几个人进同一个闸机检票通道口但次序不同,都视为不同的进站方式,那么这个家庭3个人的不同进站方式有( )种.
| A. | 24 | B. | 36 | C. | 42 | D. | 60 |
18.已知实数x,y满足不等式组$\left\{\begin{array}{l}{-3≤3x-y≤-1}\\{-1≤x+y≤1}\end{array}\right.$,若z=ax+y有最大值$\frac{5}{2}$,则实数a的值是( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | -2 | D. | -$\frac{5}{2}$ |
5.$\frac{3+i}{3-i}$=( )
| A. | $\frac{4}{5}$+$\frac{3}{5}$i | B. | $\frac{4}{5}$-$\frac{3}{5}$i | C. | $\frac{1}{2}$+$\frac{3}{2}$i | D. | $\frac{1}{2}$-$\frac{3}{2}$i |
15.执行如图的程序框图,则输出的结果为( )
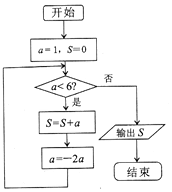

| A. | 15 | B. | 3 | C. | -11 | D. | -5 |