题目内容
20.若函数f(x)=sin$\frac{1}{2}$x的图象向左平移φ(φ>0)个单位得到函数g(x)=cos$\frac{1}{2}$x的图象,则φ的最小值是π.分析 由于f(x+φ)=g(x),利用诱导公式可得sin$\frac{1}{2}$(x+φ)=sin$\frac{1}{2}$(x+π),进而可求φ=kπ,k∈Z,结合范围φ>0,即可得解φ的最小值.
解答 解:∵f(x+φ)=g(x),即sin$\frac{1}{2}$(x+φ)=cos$\frac{1}{2}$x=-sin($\frac{1}{2}x-\frac{π}{2}$),
∴sin$\frac{1}{2}$(x+φ)=sin$\frac{1}{2}$(x+π),
∴φ=kπ,k∈Z,
∵φ>0,
∴φ的最小值是π.
故答案为:π.
点评 本题主要考查了函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象和性质的应用,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案
相关题目
11.已知直线x+ay+2=0与圆x2+y2+2x-2y+1=0有公共点,则实数a的取值范围是( )
| A. | a>0 | B. | a≥0 | C. | a≤0 | D. | a<0 |
15.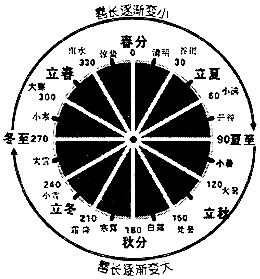 《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )
《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )
 《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )
《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )| A. | 五寸 | B. | 二尺五寸 | C. | 三尺五寸 | D. | 一丈二尺五寸 |
5.$\frac{3+i}{3-i}$=( )
| A. | $\frac{4}{5}$+$\frac{3}{5}$i | B. | $\frac{4}{5}$-$\frac{3}{5}$i | C. | $\frac{1}{2}$+$\frac{3}{2}$i | D. | $\frac{1}{2}$-$\frac{3}{2}$i |
9.设复数z1,z2在复平面内对应的点关于实轴对称,若${z_1}=\frac{1+3i}{1-i}$,则z1+z2等于( )
| A. | 4i | B. | -4i | C. | 2 | D. | -2 |
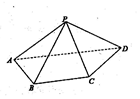 如图,已知四边形ABCD为直角梯形,∠DAB=∠ABC=90°,AB=1,AD=2BC=$\sqrt{2}$,若△PAD是以AD为底边的等腰直角三角形,且PA⊥CD.
如图,已知四边形ABCD为直角梯形,∠DAB=∠ABC=90°,AB=1,AD=2BC=$\sqrt{2}$,若△PAD是以AD为底边的等腰直角三角形,且PA⊥CD.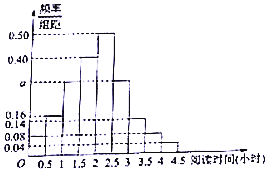 某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按图[0.0.5),[0.5,1),…,[4,4.5]分9组,制成样本的频率分布直方图如图所示.
某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按图[0.0.5),[0.5,1),…,[4,4.5]分9组,制成样本的频率分布直方图如图所示.