题目内容

19．某学校要从高一年级的752名学生中选取5名学生代表去敬老院慰问老人，若采用系统抽样方法，首先要随机剔除2名学生，再从余下的750名学生中抽取5名学生，则其中学生甲被选中的概率为（　　）
A．$\frac{1}{150}$B．$\frac{2}{752}$C．$\frac{2}{150}$D．$\frac{5}{752}$

分析 根据简单随机抽样与系统抽样方法的定义，结合概率的意义，即可判断每个人入选的概率是多少．

解答 解：根据简单随机抽样与系统抽样方法的特点，得；
每个人入选的概率都相等，且等于$\frac{5}{752}$，
故选：B．

点评 本题考查了简单随机抽样与系统抽样方法的应用问题，也考查了概率的意义问题，是基础题目

练习册系列答案
相关题目
9．某路口的红绿灯，红灯时间为30秒，黄灯时间为5秒，绿灯时间为40秒，假设你在任何时间到达该路口是等可能的，则当你到达该路口时，看见不是黄灯的概率是（　　）
A．$\frac{14}{15}$B．$\frac{1}{15}$C．.$\frac{3}{5}$D．$\frac{1}{2}$
10．设函数f（x）=ex（2x-3）-ax2+2ax+b，若函数 f（x）存在两个极值点x1，x2，且极小值点x1大于极大值点x2，则实数a的取值范围是（　　）
A．$（{0，\frac{1}{2}}）∪（{2{e^{\frac{3}{2}}}，+∞}）$B．$（{-∞，\frac{1}{2}}）∪（{4{e^{\frac{3}{2}}}，+∞}）$C．$（{-∞，2{e^{\frac{3}{2}}}}）$D．$（{-∞，1}）∪（{4{e^{\frac{3}{2}}}，+∞}）$
7．已知A，B是半径为$2\sqrt{3}$的球面上的两点，过AB作互相垂直的两个平面α、β，若α，β截该球所得的两个截面的面积之和为16π，则线段AB的长度是（　　）
A．$\sqrt{2}$B．2C．$2\sqrt{2}$D．4
14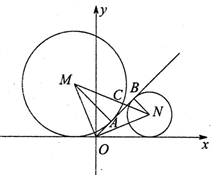．如图，圆M和圆N与直线l：y=kx分别相切于A、B，与x轴相切，并且圆心连线与l交于点C，若|OM|=|ON|且$\overrightarrow{AC}$=2$\overrightarrow{CB}$，则实数k的值为（　　）
A．1B．$\frac{3}{4}$C．$\sqrt{3}$D．$\frac{4}{3}$
4．已知实数 $a={log_2}3{，^{\;}}b=\int_1^2{（{x+\frac{1}{x}}）}dx{，^{\;}}c={log_{\frac{1}{3}}}\frac{1}{30}$，则a，b，c的大小关系是（　　）
A．a＞b＞cB．a＞c＞bC．c＞a＞bD．c＞b＞a
11．已知实数$a={log_2}3{，^{\;}}b={（{\frac{1}{3}}）^2}{，^{\;}}c={log_{\frac{1}{3}}}\frac{1}{30}$，则a，b，c的大小关系是（　　）
A．a＞b＞cB．a＞c＞bC．c＞a＞bD．c＞b＞a
15．已知函数f （x）满足：f （ p+q）=f （ p） f （q），f （1）=3，则$\frac{{{{[f（1）]}^2}+f（2）}}{f（1）}$+$\frac{{{{[f（2）]}^2}+f（4）}}{f（3）}$+$\frac{{{{[f（3）]}^2}+f（6）}}{f（5）}$+$\frac{{{{[f（4）]}^2}+f（8）}}{f（7）}$+$\frac{{{{[f（5）]}^2}+f（10）}}{f（9）}$的值为30．
16．公差不为0的等差数列{an}的前n项和为Sn，若a6=3a4，且S10=λa4，则λ的值为（　　）
A．15B．21C．23D．25

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网