题目内容
已知圆O:x2+y2=34,椭圆C:
+
=1.
(Ⅰ)若点P在圆O上,线段OP的垂直平分线经过椭圆的右焦点,求点P的横坐标;
(Ⅱ)现有如下真命题:“过圆x2+y2=52+32上任意一点Q(m,n)作椭圆
+
=1的两条切线,则这两条切线互相垂直”;“过圆x2+y2=42+72上任意一点Q(m,n)作椭圆
+
=1的两条切线,则这两条切线互相垂直”.据此,写出一般结论,并加以证明.
| x2 |
| 25 |
| y2 |
| 9 |
(Ⅰ)若点P在圆O上,线段OP的垂直平分线经过椭圆的右焦点,求点P的横坐标;
(Ⅱ)现有如下真命题:“过圆x2+y2=52+32上任意一点Q(m,n)作椭圆
| x2 |
| 52 |
| y2 |
| 32 |
| x2 |
| 42 |
| y2 |
| 72 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)设点P(x0,y0),则x02+y02=34,利用MF⊥OP,可得kOP•kMF=-1,进而可得y02+x02-8x0=0,从而可求点P的横坐标;
(Ⅱ)一般结论为:“过圆x2+y2=a2+b2上任意一点Q(m,n)作椭圆
+
=1的两条切线,则这两条切线互相垂直”,再分类讨论,借助于根的判别式,即可得出结论.
(Ⅱ)一般结论为:“过圆x2+y2=a2+b2上任意一点Q(m,n)作椭圆
| x2 |
| a2 |
| y2 |
| b2 |
解答:
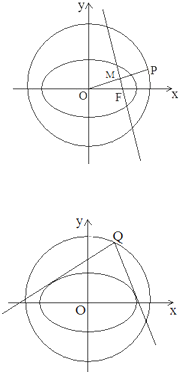 解:(Ⅰ)设点P(x0,y0),则x02+y02=34,(1)…(1分)
解:(Ⅰ)设点P(x0,y0),则x02+y02=34,(1)…(1分)
设线段OP的垂直平分线与OP相交于点M,则M(
,
),…(2分)
椭圆C:
+
=1的右焦点F(4,0),…(3分)
∵MF⊥OP,∴kOP•kMF=-1,
∴
•
=-1,
∴y02+x02-8x0=0,(2)…(4分)
由(1),(2),解得x0=
,
∴点P的横坐标为
. …(5分)
(Ⅱ)一般结论为:“过圆x2+y2=a2+b2上任意一点Q(m,n)作椭圆
+
=1的两条切线,则这两条切线互相垂直.”…(6分)
证明如下:
(ⅰ)当过点Q与椭圆
+
=1相切的一条切线的斜率不存在时,此时切线方程为x=±a,
∵点Q在圆x2+y2=a2+b2上,
∴Q(±a,±b),
∴直线y=±b恰好为过点Q与椭圆
+
=1相切的另一条切线,
∴两切线互相垂直.…(7分)
(ⅱ)当过点Q(m,n)与椭圆
+
=1相切的切线的斜率存在时,可设切线方程为y-n=k(x-m),
由
得 b2x2+a2[k(x-m)+n]2-a2b2=0,
整理得(b2+a2k2)x2+2a2k(n-km)x+a2(n-km)2-a2b2=0,…(8分)
∵直线与椭圆相切,∴△=4a4k2(n-km)2-4(b2+a2k2)[a2(n-km)2-a2b2]=0,
整理得(m2-a2)k2-2mnk+(n2-b2)=0,…(9分)
∴k1k2=
,…(10分)
∵点Q(m,n)在圆x2+y2=a2+b2上,
∴m2+n2=a2+b2,
∴m2-a2=b2-n2,
∴k1k2=-1,
∴两切线互相垂直,
综上所述,命题成立.…(13分)
 解:(Ⅰ)设点P(x0,y0),则x02+y02=34,(1)…(1分)
解:(Ⅰ)设点P(x0,y0),则x02+y02=34,(1)…(1分)设线段OP的垂直平分线与OP相交于点M,则M(
| x0 |
| 2 |
| y0 |
| 2 |
椭圆C:
| x2 |
| 25 |
| y2 |
| 9 |
∵MF⊥OP,∴kOP•kMF=-1,
∴
| y0 |
| x0 |
| ||
|
∴y02+x02-8x0=0,(2)…(4分)
由(1),(2),解得x0=
| 17 |
| 4 |
∴点P的横坐标为
| 17 |
| 4 |
(Ⅱ)一般结论为:“过圆x2+y2=a2+b2上任意一点Q(m,n)作椭圆
| x2 |
| a2 |
| y2 |
| b2 |
证明如下:
(ⅰ)当过点Q与椭圆
| x2 |
| a2 |
| y2 |
| b2 |
∵点Q在圆x2+y2=a2+b2上,
∴Q(±a,±b),
∴直线y=±b恰好为过点Q与椭圆
| x2 |
| a2 |
| y2 |
| b2 |
∴两切线互相垂直.…(7分)
(ⅱ)当过点Q(m,n)与椭圆
| x2 |
| a2 |
| y2 |
| b2 |
由
|
整理得(b2+a2k2)x2+2a2k(n-km)x+a2(n-km)2-a2b2=0,…(8分)
∵直线与椭圆相切,∴△=4a4k2(n-km)2-4(b2+a2k2)[a2(n-km)2-a2b2]=0,
整理得(m2-a2)k2-2mnk+(n2-b2)=0,…(9分)
∴k1k2=
| n2-b2 |
| m2-a2 |
∵点Q(m,n)在圆x2+y2=a2+b2上,
∴m2+n2=a2+b2,
∴m2-a2=b2-n2,
∴k1k2=-1,
∴两切线互相垂直,
综上所述,命题成立.…(13分)
点评:求圆锥曲线的方程一般利用待定系数法;解决直线与圆锥曲线的关系问题,一般将直线的方程与圆锥曲线方程联立得到二次方程,再利用根与系数的关系找突破口.

练习册系列答案
相关题目
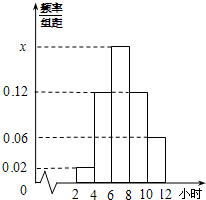 某校为了解学生寒假期间的学习情况,从初中及高中各班共抽取了50名学生,对他们每天平均学习时间进行统计.请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题:
某校为了解学生寒假期间的学习情况,从初中及高中各班共抽取了50名学生,对他们每天平均学习时间进行统计.请根据下面的各班人数统计表和学习时间的频率分布直方图解决下列问题: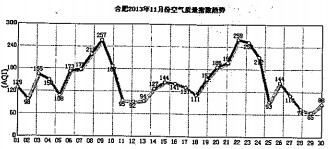 合肥市环保总站对2013年11月合肥市空气质量指数发布如图趋势图.
合肥市环保总站对2013年11月合肥市空气质量指数发布如图趋势图.