Question

如图，ABC为一直角三角形草坪，其中∠C=90°，BC=2米，AB=4米，为了重建草坪，设计师准备了两套方案：

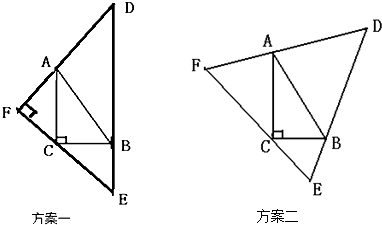
方案一：扩大为一个直角三角形，其中斜边DE过点B，且与AC平行，DF过点A，EF过点C；
方案二：扩大为一个等边三角形，其中DE过点B，DF过点A，EF过点C．
（1）求方案一中三角形DEF面积S₁的最小值；
（2）求方案二中三角形DEF面积S₂的最大值．

Answer 1

考点：基本不等式在最值问题中的应用

专题：综合题,不等式的解法及应用

分析：（1）在方案一：在三角形AFC中，设∠ACF=α，α∈（0，

π

2

），表示出三角形DEF面积S₁，利用基本不等式求出最小值；
（2）在方案二：在三角形DBA中，设∠DBA=β，β∈（0，

2π

3

），表示出三角形DEF面积S₁，利用辅助角公式求出最小值．

解答： 解：（1）在方案一：在三角形AFC中，设∠ACF=α，α∈（0，

π

2

），
则AF=2

3

sinα，FC=2

3

cosα，…（2分）
因为DE∥AC，所以∠E=α，EC=

2

sinα

，
且

FA

AD

=

FC

CE

，即

2 3 sinα

AD

=

2 3 cosα

2 sinα

，…（4分）
解得AD=

2

cosα

，…（6分）
所以S1=

1

2

(2

3

sinα+

2

cosα

)(2

3

cosα+

2

sinα

)=3(sin2α+

4

3sin2α

)+4

3

，
所以当sin2α=1，即α=45°时，S₁有最小值7+4

3

． …（8分）
（2）在方案二：在三角形DBA中，设∠DBA=β，β∈（0，

2π

3

），则

DB

sin(120°-β)

=

AB

sin60°

，
解得DB=

8

3

sin(120°-β)，…（10分）
三角形CBE中，有

EB

sinβ

=

CB

sin60°

，解得EB=

4

3

sinβ，…（12分）
则等边三角形的边长为

8

3

sin(120°-β)+

4

3

sinβ=

4

3

(2sinβ+

3

cosβ)，…（14分）
所以边长的最大值为

4 7

3

，所以面积S₂的最大值为

3

4

×(

4 7

3

)2=

28 3

3

．…（16分）

点评：本题考查基本不等式在最值问题中的应用，考查学生利用数学知识解决实际问题，属于中档题．