题目内容
13.已知数列{an}的前n项和Sn满足:Sn=an2+bn,且a1=1,a2=3.(I)求数列{an}的通项公式;
(Ⅱ)记bn=2${\;}^{{a}_{n}}$,数列{bn}的前n项和Tn,求证:Tn≥2.
分析 (I)通过Sn=an2+bn及a1=1、a2=3求出a、b的值,进而利用当n≥2时an=Sn-Sn-1计算即得结论;
(Ⅱ)通过(I)可知bn=$\frac{1}{2}$•4n,利用等比数列的求和公式计算、放缩即得结论.
解答 (I)解:∵Sn=an2+bn,且a1=1,a2=3,
∴$\left\{\begin{array}{l}{1=a+b}\\{1+3=4a+2b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$,
∴Sn=n2,
当n≥2时,an=Sn-Sn-1=n2-(n-1)2=2n-1,
又∵a1=1满足上式,
∴数列{an}的通项公式an=2n-1;
(Ⅱ)证明:由(I)可知bn=22n-1=$\frac{1}{2}$•4n,
∴Tn=$\frac{1}{2}$•$\frac{4(1-{4}^{n})}{1-4}$=$\frac{2}{3}$(4n-1)≥$\frac{2}{3}$(4-1)=2.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
3.若一个高为4,底面边长为2的正四棱锥的顶点都在同一个球面上,则该球的表面积为( )
| A. | $\frac{81}{4}$π | B. | 16π | C. | 9π | D. | $\frac{27}{4}$π |
1.在复平面内,复数$\frac{2}{1-i}$+2i2对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
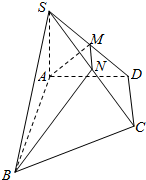 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,CD=DA=a,AB=2a,SA⊥平面ABCD,且SA=a
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,CD=DA=a,AB=2a,SA⊥平面ABCD,且SA=a