题目内容
18.已知以点C(a,$\frac{2}{a}$)(a>0)为圆心的圆与x轴交于点O,A,与y轴交于点O、B,其中O为原点.(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M,N,若OM=ON,求圆C的方程.
分析 (1)设出圆C的方程,求得A、B的坐标,再根据S△AOB=$\frac{1}{2}$OA•OB,计算可得结论.
(2)设MN的中点为H,则CH⊥MN,根据C、H、O三点共线,KMN=-2,由直线OC的斜率k=$\frac{\frac{2}{a}}{a}$=$\frac{1}{2}$,求得a的值,可得所求的圆C的方程.
解答 (1)证明:由题设知,圆C的方程为(x-a)2+(y-$\frac{2}{a}$)2=a2+$\frac{4}{{a}^{2}}$,
化简得x2-2ax+y2-$\frac{4}{a}$y=0.
当y=0时,x=0或2a,则A(2a,0);
当x=0时,y=0或$\frac{4}{a}$,则B(0,$\frac{4}{a}$),
∴S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$|2a|•|$\frac{4}{a}$|=4为定值.
(2)解∵OM=ON,则原点O在MN的中垂线上,设MN的中点为H,则CH⊥MN,
∴C、H、O三点共线,KMN=-2,则直线OC的斜率k=$\frac{\frac{2}{a}}{a}$=$\frac{1}{2}$,
∴a=2或a=-2.
∴圆心为C(2,1)或C(-2,-1),
∴圆C的方程为(x-2)2+(y-1)2=5或(x+2)2+(y+1)2=5.
由于当圆方程为(x+2)2+(y+1)2=5时,直线2x+y-4=0到圆心的距离d>r,
此时不满足直线与圆相交,故舍去,
∴所求的圆C的方程为(x-2)2+(y-1)2=5.
点评 本题主要考查求圆的标准方程,两条直线垂直的性质,属于中档题.

练习册系列答案
相关题目
8.以直线x=1为准线的抛物线的标准方程是( )
| A. | y2=2x | B. | x2=4y | C. | y2=-4x | D. | y2=-4x |
8.函数f(x)=(x-1)2+1(x>1)的反函数为( )
| A. | y=1+$\sqrt{x-1}$(x>1) | B. | y=1-$\sqrt{x-1}$(x>1) | C. | y=1+$\sqrt{x-1}$(x≥1) | D. | y=1-$\sqrt{x-1}$(x≥1) |
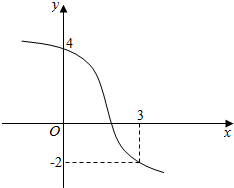 已知函数f(x)的部分图象如图所示,若不等式-2<f(x+t)<4的解集为(-1,2),则实数t的值为-1.(写过程)
已知函数f(x)的部分图象如图所示,若不等式-2<f(x+t)<4的解集为(-1,2),则实数t的值为-1.(写过程)