题目内容
16.已知抛物线C的顶点为坐标原点,对称轴为x轴,且过点(1,1).(1)求抛物线C的方程;
(2)若斜率为2的直线l与抛物线C相切于点A,求直线l的方程和切点A的坐标.
分析 (1)设出抛物线方程,代入点的坐标,可得抛物线C的方程;
(2)直线与抛物线方程联立,利用判别式为0,求出b,即可求直线l的方程和切点A的坐标.
解答 解:(1)由C的顶点为坐标原点,对称轴为x轴,可设:C:y2=2px
∵y2=2px过点(1,1),∴1=2p,解得$p=\frac{1}{2}$…(4分)
∴抛物线C的方程为y2=x…(5分)
(2)∵直线l的斜率为2,∴设l:y=2x+b
由$\left\{\begin{array}{l}y=2x+b\\{y^2}=x\end{array}\right.$得2y2-y+b=0,…(7分)
∵l与C相切,∴△=(-1)2-8b=0,∴$b=\frac{1}{8}$…(8分)
把$b=\frac{1}{8}$代入y=2x+b得,$y=2x+\frac{1}{8}$,即l:16x-8y+1=0…(10分)
把$b=\frac{1}{8}$代入2y2-y+b=0得$y=\frac{1}{4}$,∴$x=\frac{1}{16}$,∴$A({\frac{1}{16},\frac{1}{4}})$…(12分)
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.函数f(x)=ex(2-|x|)-1的零点个数为( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
11.设抛物线y2=8x的焦点为F,M是抛物线上一点,N(2,2),则|MF|+|MN|的取值范围是( )
| A. | (0,4] | B. | [4,+∞) | C. | (0,2] | D. | [2,+∞) |
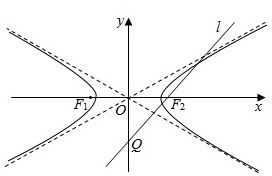 如图,双曲线Γ:$\frac{{x}^{2}}{3}$-y2=1的左、右焦点分别为F1,F2,过F2作直线l交y轴于点Q.
如图,双曲线Γ:$\frac{{x}^{2}}{3}$-y2=1的左、右焦点分别为F1,F2,过F2作直线l交y轴于点Q.