题目内容
14.已知圆O1和圆O2都经过点A(0,1),若两圆与直线4x-3y+5=0及y+1=0均相切,则|O1O2|=$\sqrt{5}$.分析 由题意画出图形,可得两圆中一个圆的圆心在坐标原点,由已知列式求出另一圆心坐标,则答案可求.
解答 解:如图,∵原点O到直线4x-3y+5=0的距离d=$\frac{|5|}{\sqrt{{4}^{2}+(-3)^{2}}}=1$,到直线y=-1的距离为1,且到(0,1)的距离为1,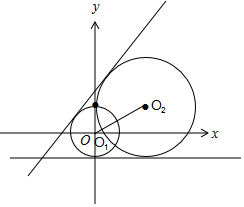
∴圆O1和圆O2的一个圆心为原点O,不妨看作是圆O1,
设O2(a,b),则由题意:
$\left\{\begin{array}{l}{b+1=\sqrt{{a}^{2}+(b-1)^{2}}}\\{b+1=\frac{|4a-3b+5|}{\sqrt{{4}^{2}+(-3)^{2}}}}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$.
∴$|{O}_{1}{O}_{2}|=\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查直线与圆、圆与圆位置关系的应用,考查数形结合的解题思想方法,训练了点到直线距离公式的应用,是中档题.

练习册系列答案
相关题目
6.在2016年巴西里约奥运会期间,6名游泳队员从左至右排成一排合影留念,最左边只能排甲或乙,最右端不能排甲,则不同的排法种数为( )
| A. | 216 | B. | 108 | C. | 432 | D. | 120 |
19.设函数$f(x)=\sqrt{lnx+x+m}$,若曲线$y=\frac{1-e}{2}cosx+\frac{1+e}{2}$上存在(x0,y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
| A. | [0,e2-e+1] | B. | [0,e2+e-1] | C. | [0,e2+e+1] | D. | [0,e2-e-1] |
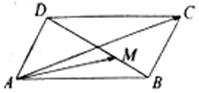 如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.
如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.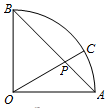 如图,扇形AOB的圆心角为90°,点P在弦AB上,且OP=$\sqrt{2}$AP,延长OP交弧AB于点C,现向该扇形内随机投一点,则该点落在扇形AOC内的概率为$\frac{1}{3}$.
如图,扇形AOB的圆心角为90°,点P在弦AB上,且OP=$\sqrt{2}$AP,延长OP交弧AB于点C,现向该扇形内随机投一点,则该点落在扇形AOC内的概率为$\frac{1}{3}$.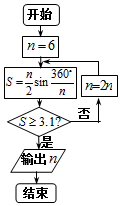 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为(参考数据:sin15°=0.2588,sin7.5°=0.1305)( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为(参考数据:sin15°=0.2588,sin7.5°=0.1305)( )