题目内容
19.设函数$f(x)=\sqrt{lnx+x+m}$,若曲线$y=\frac{1-e}{2}cosx+\frac{1+e}{2}$上存在(x0,y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )| A. | [0,e2-e+1] | B. | [0,e2+e-1] | C. | [0,e2+e+1] | D. | [0,e2-e-1] |
分析 求出y0的范围,证明f(y0)=y0,得出f(x)=x在[1,e]上有解,再分离参数,利用函数单调性求出m的范围.
解答 解:∵-1≤cosx≤1,∴$\frac{1-e}{2}cosx+\frac{1+e}{2}$的最大值为e,最小值为1,∴1≤y0≤e,
显然f(x)=$\sqrt{lnx+x+m}$是增函数,
(1)若f(y0)>y0,则f(f(y0))>f(y0)>y0,与f(f(y0))=y0矛盾;
(2)若f(y0)<y0,则f(f(y0))<f(y0)<y0,与f(f(y0))=y0矛盾;
∴f(y0)=y0,
∴y0为方程f(x)=x的解,即方程f(x)=x在[1,e]上有解,
由f(x)=x得m=x2-x-lnx,
令g(x)=x2-x-lnx,x∈[1,e],
则g′(x)=2x-1-$\frac{1}{x}$=$\frac{2{x}^{2}-x-1}{x}$=$\frac{(2x+1)(x-1)}{x}$,
∴当x∈[1,e]时,g′(x)≥0,
∴g(x)在[1,e]上单调递增,
∴gmin(x)=g(1)=0,gmax(x)=g(e)=e2-e-1,
∴0≤m≤e2-e-1.
故选D.
点评 本题考查了函数零点与函数单调性的关系,函数单调性的判断与最值计算,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
11.设集合A={x|x2-1<0},B={x|y=ln(x-1)},则A∪B=( )
| A. | (-1,1) | B. | (-1,+∞) | C. | (-1,1)∪(1,+∞) | D. | (1,+∞) |
4.执行如图所示的程序框图,若输入的k,b,r的值分别为2,2,4,则输出i的值是( )
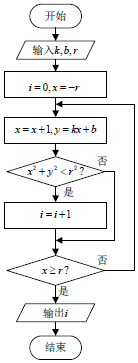

| A. | 4 | B. | 3 | C. | 6 | D. | 7 |
11.$\int{\begin{array}{l}{\frac{π}{4}}\\ 0\end{array}}({sinx-acosx})dx=-\frac{{\sqrt{2}}}{2}$,则实数a等于( )
| A. | 1 | B. | $\sqrt{2}$ | C. | -1 | D. | $-\sqrt{3}$ |
9.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线方程为x-ay=0,曲线C的一个焦点与抛物线y2=-8x的焦点重合,则双曲线的离心率为( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{10}$ |