题目内容
4.函数f(x)=$\frac{{x}^{2}}{x-1}$(x>1)的最小值为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 把函数解析式变形,然后利用基本不等式求最值.
解答 解:∵x>1,
∴f(x)=$\frac{{x}^{2}}{x-1}$=$\frac{(x-1)^{2}+2(x-1)+1}{x-1}$=$(x-1)+\frac{1}{x-1}+2$$≥2\sqrt{(x-1)•\frac{1}{x-1}}+2=4$.
当且仅当x-1=$\frac{1}{x-1}$,即x=2时上式取等号.
∴函数f(x)=$\frac{{x}^{2}}{x-1}$(x>1)的最小值为4.
故选:A.
点评 本题考查函数的最值及其几何意义,训练了利用基本不等式求最值,是中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
10.在等差数列{an}中,a3=0,a7-2a4=-1,则公差d等于( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | 2 | D. | -$\frac{1}{2}$ |
15.6个电子产品中有2个次品,4个合格品,每次从中任取一个测试,测试完后不放回,直到两个次品都找到为止,那么测试次数X的均值为( )
| A. | $\frac{17}{15}$ | B. | $\frac{11}{15}$ | C. | $\frac{5}{3}$ | D. | $\frac{64}{15}$ |
19.一个三角形的三个内角A,B,C成等差数列,则cosB=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
16.若复数z满足(3-4i)z=|4+3i|,则$\overline{z}$的虚部为( )
| A. | $-\frac{4}{5}i$ | B. | $-\frac{4}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{5}i$ |
14.在△ABC中,已知b=$\sqrt{2},c=1,B={45°}$,则此三角形有几个解( )
| A. | 0 | B. | 1 | C. | 2 | D. | 不确定 |
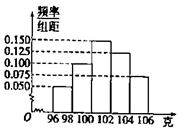 某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),(104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
某工厂对一批产品进行了抽样检测,如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),(104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )