题目内容
11.向△ABC内任意投一点P,若△ABC面积为s,则△PBC的面积小于等于$\frac{s}{2}$的概率为$\frac{3}{4}$.分析 由在△ABC的中位线上任取一点P,则△PBC的面积等于$\frac{s}{2}$,即满足条件的点P构成的区域,再根据面积比,得到结果.
解答 解:记事件A={△PBC的面积小于$\frac{s}{2}$},
基本事件空间是三角形ABC的面积,(如图)
事件A的几何度量为图中阴影部分的面积(DE是三角形的中位线),
因为阴影部分的面积是整个三角形面积的$\frac{3}{4}$,
所以P(A)=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$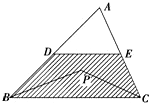
点评 本题考查了几何概型,解答此题的关键在于明确测度比是面积比.对于几何概型常见的测度是长度之比,面积之比,体积之比,角度之比,要根据题意合理的判断和选择是哪一种测度进行求解.属于中档题.

练习册系列答案
相关题目
2.已知函数f(x)=$\left\{\begin{array}{l}{x,x≤0}\\{{x}^{2}-x,x>0}\end{array}\right.$,若函数g(x)=f(x)-m有三个不同的零点,则实数m的取值范围为( )
| A. | $({-\frac{1}{4},0})$ | B. | $({-\frac{1}{4},0}]$ | C. | $[{-\frac{1}{2},1}]$ | D. | $[{-\frac{1}{2},1})$ |
19.一个三角形的三个内角A,B,C成等差数列,则cosB=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
16.若复数z满足(3-4i)z=|4+3i|,则$\overline{z}$的虚部为( )
| A. | $-\frac{4}{5}i$ | B. | $-\frac{4}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{5}i$ |
1.若a,b∈R,且(a+i)i=b+i,则( )
| A. | a=1,b=1 | B. | a=-1,b=1 | C. | a=1,b=-1 | D. | a=-1,b=-1 |