题目内容
9.过曲线y=$\frac{1}{8}$x4上一点P(2,2)的切线的斜率是( )| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
分析 求出函数的导数,由导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,代入x=2,即可得到所求斜率.
解答 解:y=$\frac{1}{8}$x4的导数为y′=$\frac{1}{2}$x3,
即有曲线y=$\frac{1}{8}$x4上一点P(2,2)的切线的斜率为:
k=$\frac{1}{2}$×23=4.
故选:C.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,考查运算能力,属于基础题.

练习册系列答案
相关题目
19.函数f(x)=sin2x和函数g(x)的部分图象如图所示,则函数g(x)的解析式可以是( )

| A. | g(x)=sin(2x-$\frac{π}{3}}$) | B. | g(x)=sin(2x+$\frac{2π}{3}}$) | C. | g(x)=cos(2x+$\frac{5π}{6}}$) | D. | g(x)=cos(2x-$\frac{π}{6}}$) |
4.直线x=1,x=2,y=0及曲线y=x3围成的平面图形的面积为( )
| A. | $\sum_{i=1}^{n}$$\frac{1}{n}$(1+$\frac{i}{n}$)3 | B. | ${∫}_{1}^{2}$x3dx | C. | ${∫}_{2}^{1}$x3dx | D. | 1 |
18.下列各组向量中互相垂直的是( )
| A. | $\overrightarrow{a}$=(-3,5),$\overrightarrow{b}$=(-1,5) | B. | $\overrightarrow{a}$=(3,2),$\overrightarrow{b}$=(-3,-2) | C. | $\overrightarrow{a}$=(3,4),$\overrightarrow{b}$=(4,-3) | D. | $\overrightarrow{a}$=(-3,3),$\overrightarrow{b}$=(-1,1) |
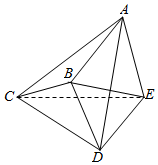 在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.
在如图所示的几何体ABCDE中,AE⊥平面DCE,BE=$\sqrt{6}$,DC=4,BD=2,CE=2$\sqrt{3}$,∠BCD=30°,CE⊥AD.