题目内容
下列函数中既是奇函数，又在（0，+∞）上单调递增的是（ ）
| A、y=sinx | ||
B、y=-x2+
| ||
| C、y=x3+3x | ||
| D、y=e|x| |
考点：函数奇偶性的判断,函数单调性的判断与证明
专题：函数的性质及应用
分析：对于四个选项分别分析，利用奇偶函数的定义及性质解答．
解答：
解：对于A，是奇函数，但是在R是周期函数，不单调；
对于B，f（-x）=-x2-
≠f（x），也不等于-f（x），所以是非奇非偶的函数；
对于D，f（-x）=e|-x|=e|x|=f（x），是偶函数；
故选：C．
对于B，f（-x）=-x2-
| 1 |
| x |
对于D，f（-x）=e|-x|=e|x|=f（x），是偶函数；
故选：C．
点评：本题考查了函数的奇偶性的判断以及单调性的判断．
练习册系列答案
相关题目
给出下列图象，其中可能为函数f（x）=x4+ax3+cx+d（a，b，c，d∈R）的图象是（ ）
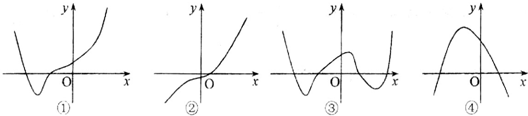
| A、①③ | B、①② | C、③④ | D、②④ |
如图，电键A、B、C、D闭合的概率分别为p1、p2、p3、p4，且彼此独立，求灯泡亮的概率．在△ABC中，角A，B，C，的对边分别为a，b，c，若（a2+c2-b2）tanB=
ac，则角B的值为（ ）
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若集合A={x|-2＜x＜1}，B={x|0＜x＜2}，则集合A∪B等于（ ）
| A、{x|-1＜x＜1} |
| B、{x|-2＜x＜1} |
| C、{x|-2＜x＜2} |
| D、{x|0＜x＜1} |