题目内容
9.若f(x)是偶函数,且在[0,+∞)上函数$f(x)=\left\{\begin{array}{l}{({\frac{3}{4}})^x},x<1\\ 3-\frac{9}{4}x,x≥1\end{array}\right.$,则$f({-\frac{3}{2}})$与$f({{a^2}+2a+\frac{5}{2}})$的大小关系是( )| A. | $f({-\frac{3}{2}})>f({{a^2}+2a+\frac{5}{2}})$ | B. | $f({-\frac{3}{2}})<f({{a^2}+2a+\frac{5}{2}})$ | C. | $f({-\frac{3}{2}})≥f({{a^2}+2a+\frac{5}{2}})$ | D. | $f({-\frac{3}{2}})≤f({{a^2}+2a+\frac{5}{2}})$ |
分析 根据题意,分析函数f(x)在区间[0,+∞)的单调性,由函数为偶函数可得$f({-\frac{3}{2}})$=f($\frac{3}{2}$),分析可得a2+2a+$\frac{5}{2}$=(a+1)2+$\frac{3}{2}$≥$\frac{3}{2}$,结合函数在[0,+∞)的单调性分析可得答案.
解答 解:根据题意,在[0,+∞)上函数$f(x)=\left\{\begin{array}{l}{({\frac{3}{4}})^x},x<1\\ 3-\frac{9}{4}x,x≥1\end{array}\right.$,
则函数在区间(1,+∞)上为减函数,
若f(x)是偶函数,则$f({-\frac{3}{2}})$=f($\frac{3}{2}$),
又由a2+2a+$\frac{5}{2}$=(a+1)2+$\frac{3}{2}$≥$\frac{3}{2}$,
则有f($\frac{3}{2}$)≥f(a2+2a+$\frac{5}{2}$),
即f(-$\frac{3}{2}$)≥f(a2+2a+$\frac{5}{2}$),
故选:C.
点评 本题考查函数奇偶性与单调性的综合应用,关键是分析函数在区间[0,+∞)上的单调性.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
17.已知i是虚数单位,复数z满足(1-i)z=i,则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
6.已知函数f(x)=asinx+bcosx(x∈R),若x=x0是函数f(x)的一条对称轴,且tanx0=3,则点(a,b)所在的直线为( )
| A. | x-3y=0 | B. | x+3y=0 | C. | 3x-y=0 | D. | 3x+y=0 |
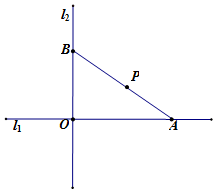 如图所示,互相垂直的两条道路l1、l2相交于O点,点P与l1、l2的距离分别为2千米、3千米,过点P建一条直线道路AB,与l1、l2分别交于A、B两点.
如图所示,互相垂直的两条道路l1、l2相交于O点,点P与l1、l2的距离分别为2千米、3千米,过点P建一条直线道路AB,与l1、l2分别交于A、B两点. 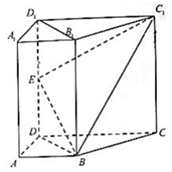 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.