题目内容
已知数列{an}满足:a1=m,m为正整数,an+1=
,若a6=1,则m所有可能的取值为( )
|
| A、{4,5} |
| B、{4,32} |
| C、{4,5,32} |
| D、{5,32} |
考点:数列的概念及简单表示法
专题:等差数列与等比数列
分析:a6=1,可得a5必为偶数,因此a6=
=1,解得a5=2.当a4为偶数时,a5=
,解得a4=4;当a4为奇数时,a5=3a4+1=2,解得a4=-
,舍去.依此类推即可得出.
| a5 |
| 2 |
| a4 |
| 2 |
| 1 |
| 3 |
解答:
解:∵a6=1,
∴a5必为偶数,∴a6=
=1,解得a5=2.
当a4为偶数时,a5=
,解得a4=4;当a4为奇数时,a5=3a4+1=2,解得a4=-
,舍去.
∴a4=4.
当a3为偶数时,a4=
=4,解得a3=8;当a3为奇数时,a4=3a3+1=4,解得a3=1.
当a3=8时,当a2为偶数时,a3=
=8,解得a2=16;当a2为奇数时,a3=3a2+1=8,解得a3=
,舍去.
当a3=1时,当a2为偶数时,a3=
=1,解得a2=2;当a2为奇数时,a3=3a2+1=1,解得a2=0,舍去.
当a2=16时,当a1为偶数时,a2=
=16,解得a1=32=m;当a1为奇数时,a2=3a1+1=16,解得a1=5=m.
当a2=2时,当a1为偶数时,a2=
=2,解得a1=4=m;当a1为奇数时,a2=3a1+1=2,解得a1=
,舍去.
综上可得m=4,5,32.
故选:C.
∴a5必为偶数,∴a6=
| a5 |
| 2 |
当a4为偶数时,a5=
| a4 |
| 2 |
| 1 |
| 3 |
∴a4=4.
当a3为偶数时,a4=
| a3 |
| 2 |
当a3=8时,当a2为偶数时,a3=
| a2 |
| 2 |
| 7 |
| 3 |
当a3=1时,当a2为偶数时,a3=
| a2 |
| 2 |
当a2=16时,当a1为偶数时,a2=
| a1 |
| 2 |
当a2=2时,当a1为偶数时,a2=
| a1 |
| 2 |
| 1 |
| 3 |
综上可得m=4,5,32.
故选:C.
点评:本题考查了分段数列的求值、分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
若(m2-4)x+(m2-4m+3)y+1=0表示直线,则( )
| A、m≠±2且m≠1,m≠3 |
| B、m≠±2 |
| C、m≠1且m≠3 |
| D、m∈R |
已知奇函数f(x)为R上的减函数,则关于a的不等式f(a2)+f(2a)>0的解集是( )
| A、(-2,0 ) |
| B、( 0,2 ) |
| C、(-2,0 )∪( 0,2 ) |
| D、(-∞,-2 )∪( 0,+∞) |
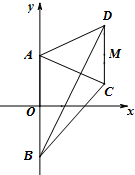 如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=
如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|= 如图,一艘船从A点出发以2
如图,一艘船从A点出发以2 函数f(x)=3sin(2x+
函数f(x)=3sin(2x+