题目内容
某三棱锥的三视图如图所示，这个三棱锥最长棱的棱长是（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三视图可知：原三棱锥为P-ABC．其中PA⊥底面ABC，AC⊥CB，PA=AC=BC=1．可得这个三棱锥最长棱的棱长是PB．
解答：
解：由三视图可知：原三棱锥为
P-ABC．
其中PA⊥底面ABC，AC⊥CB，PA=AC=BC=1．
∴这个三棱锥最长棱的棱长是PB=
=
．
故选：C．
P-ABC．其中PA⊥底面ABC，AC⊥CB，PA=AC=BC=1．
∴这个三棱锥最长棱的棱长是PB=
| PA2+AB2 |
| 3 |
故选：C．
点评：本题考查了三视图的有关知识、三棱锥的有关计算，属于基础题．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
相关题目
已知一个几何体的三视图及长度如图所示，则该几何体的体积是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
在边长为1的等边△ABC中，D，E分别在边BC与AC上，且
=
，2
=
，则
•
=（ ）
| BD |
| DC |
| AE |
| EC |
| AD |
| BE |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
如图为一个几何体的三视图，则该几何体的外接球的表面积为（ ）
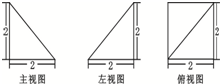
| A、4π | B、8π |
| C、12π | D、16π |
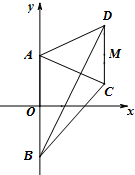如图，梯形ABCD的底边AB在y轴上，原点O为AB的中点，|AB|=