题目内容
在R上定义的函数f(x)是偶函数,且f(x)=f(2-x),若f(x)在区间x∈[1,2)是减函数,则函数 f(x)( )
| A、在区间[-2,-1]上是减函数,区间[3,4]上是增函数 |
| B、在区间[-2,-1]上是减函数,区间[3,4]上是减函数 |
| C、在区间[-2,-1]上是增函数,区间[3,4]上是增函数 |
| D、在区间[-2,-1]上是增函数,区间[3,4]上是减函数 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:先再根据函数f(x)是偶函数,得到函数f(x)的图象关于y轴对称,根据条件f(x)=f(2-x),函数f(x)的图象关于直线x=1对称,由函数的对称性研究还可得到函数的周期性,利用已知f(x)在区间x∈[1,2)是减函数,得到函数f(x)在相关区间上的单调性,得到本题结论.
解答:
解:∵定义的函数f(x)是偶函数,
∴f(-x)=f(x),
函数f(x)的图象关于y轴对称,
∴f(x)在区间x∈[1,2]是减函数,
∴f(x)在区间x∈[-2,-1]是增函数
∵f(x)=f(2-x),
∴f(1+x)=f[2-(1+x)]=f(1-x),
函数f(x)的图象关于直线x=1对称.
∴f(x)在区间x∈[3,4]是减函数.
故选D.
∴f(-x)=f(x),
函数f(x)的图象关于y轴对称,
∴f(x)在区间x∈[1,2]是减函数,
∴f(x)在区间x∈[-2,-1]是增函数
∵f(x)=f(2-x),
∴f(1+x)=f[2-(1+x)]=f(1-x),
函数f(x)的图象关于直线x=1对称.
∴f(x)在区间x∈[3,4]是减函数.
故选D.
点评:本题考查了函数的奇偶性与图象的对称性、单调性的关系,本题难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图为一个几何体的三视图,则该几何体的外接球的表面积为( )
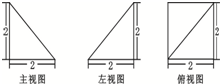

| A、4π | B、8π |
| C、12π | D、16π |
已知向量
=(1,2),
=(1+m,m-1),若
∥
,则实数m的值为( )
| a |
| b |
| a |
| b |
| A、3 | B、-3 | C、2 | D、-2 |
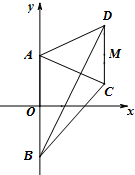 如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=
如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=