题目内容
设M,m分别是f(x)在区间[a,b]上的最大值和最小值,则m(b-a)≤∫abf(x)dx≤M(b-a),由上述估值定理,估计定积分
2-x2dx的取值范围是 .
| ∫ | 2 -1 |
考点:定积分,函数的最值及其几何意义
专题:导数的综合应用
分析:首先求出被积函数的最值,然后由估值定理求定积分的范围.
解答:
解:由题意2 -x2在[-1,2]最大值为1,最小值为
,所以
≤
2-x2dx≤3;
故答案为:[
,3].
| 1 |
| 16 |
| 3 |
| 16 |
| ∫ | 2 -1 |
故答案为:[
| 3 |
| 16 |
点评:本题考查了定积分的运用,关键是正确理解估值定理,属于中档题.

练习册系列答案
相关题目
已知向量
=(1,2),
=(1+m,m-1),若
∥
,则实数m的值为( )
| a |
| b |
| a |
| b |
| A、3 | B、-3 | C、2 | D、-2 |
已知集合A={0,1,2,3,4},B={(x,y)|x∈A,y∈A,x-y∈A},则B中所含元素的个数为( )
| A、5 | B、6 | C、10 | D、15 |
若(m2-4)x+(m2-4m+3)y+1=0表示直线,则( )
| A、m≠±2且m≠1,m≠3 |
| B、m≠±2 |
| C、m≠1且m≠3 |
| D、m∈R |
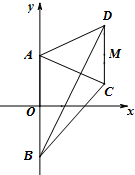 如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=
如图,梯形ABCD的底边AB在y轴上,原点O为AB的中点,|AB|=