题目内容
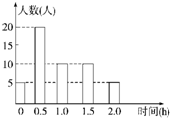某校为了解学生的课外阅读情况，随机调查了50名学生，得到他们在某一天课外阅读所用时间的数据，结果用条形图表示如下．根据条形图可得这50名学生这一天平均每人的课外阅读时间为（ ）| A、0.6 h |
| B、0.9 h |
| C、1.0 h |
| D、1.5 h |
考点：频率分布直方图
专题：概率与统计
分析：根据频率分布直方图，结合平均数的概念，求出数据的平均数即可．
解答：
解：根据频率分布直方图，得；
平均数是
=
×（5×0+20×0.5+10×1+10×1.5+5×2）=0.9；
即这50名学生一天平均每人的课外阅读时间为0.9h．
故选：B．
平均数是
. |
| x |
| 1 |
| 50 |
即这50名学生一天平均每人的课外阅读时间为0.9h．
故选：B．
点评：本题考查了利用频率分布直方图求数据的平均数的问题，解题时应结合平均数的概念进行解答，是基础题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
在长方形ABCD中，AB=2，AD=1，则
•
=（ ）
| AC |
| CD |
| A、-2 | B、2 | C、4 | D、-4 |
函数f（x）是定义在区间[-5，5]上的偶函数，且在[0，5]上是单调函数，f（1）＜f（3），则下列各式一定成立的是（ ）
| A、f（0）＞f（5） |
| B、f（3）＜f（2） |
| C、f（-1）＞f（3） |
| D、f（-2）＞f（1） |
若2弧度的圆心角所对的弧长为2cm，则这个圆心角所夹的扇形的面积是（ ）
| A、4 cm2 |
| B、2 cm2 |
| C、4π cm2 |
| D、1 cm2 |
掷一枚质地均匀的硬币3次，恰有2次正面向上的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合A={x∈R|x+y=2}，集合B={x∈R|x≤2}，则A∩B=（ ）
| A、{2} | B、φ | C、A | D、B |
cos2
-sin2
=（ ）
| π |
| 12 |
| π |
| 12 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|