题目内容
8.若正数x,y,z满足6x+y+5z=2,则$\frac{1}{y+2z}+\frac{2}{2x+z}$的最小值为$\frac{7}{2}$+$\sqrt{6}$.分析 $\frac{1}{y+2z}+\frac{2}{2x+z}$=$\frac{6x+y+5z}{2(y+2z)}$+$\frac{6x+y+5z}{2x+z}$,从而利用基本不等式证明.
解答 解:$\frac{1}{y+2z}+\frac{2}{2x+z}$
=$\frac{6x+y+5z}{2(y+2z)}$+$\frac{6x+y+5z}{2x+z}$
=$\frac{3(2x+z)+y+2z}{2(y+2z)}$+$\frac{3(2x+z)+y+2z}{2x+z}$
=$\frac{3}{2}$•$\frac{2x+z}{y+2z}$+$\frac{1}{2}$+3+$\frac{y+2z}{2x+z}$
≥2$•\sqrt{\frac{3}{2}}$+$\frac{7}{2}$=$\frac{7}{2}$+$\sqrt{6}$;
(当且仅当$\frac{3}{2}$•$\frac{2x+z}{y+2z}$=$\frac{y+2z}{2x+z}$时,等号成立);
故答案为:$\frac{7}{2}$+$\sqrt{6}$.
点评 本题考查了学生的化简运算能力及基本不等式的应用.

练习册系列答案
相关题目
3.“a=2”是“直线2x-3y=0与直线3x+ay+1=0垂直”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
13.设实数x,y满足不等式$\left\{\begin{array}{l}{x+y-11≤0}\\{3x-y+3≤0}\\{y≥0}\\{\;}\end{array}\right.$,则z=3x+y的最大值为( )
| A. | -3 | B. | 11 | C. | 15 | D. | 不存在 |
18.已知sinα=-$\frac{4}{5}$,α∈(π,$\frac{3π}{2}$),则tan$\frac{α}{2}$等于( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$或2 | D. | -2或$\frac{1}{2}$ |
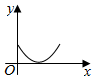
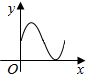
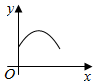
 如图,圆与两坐标轴分别切于A,B两点,圆上一动点P从A开始沿圆周按逆时针方向匀速旋转回到A点,则△OBP的面积随时间变化的图象符合( )
如图,圆与两坐标轴分别切于A,B两点,圆上一动点P从A开始沿圆周按逆时针方向匀速旋转回到A点,则△OBP的面积随时间变化的图象符合( )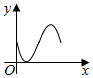
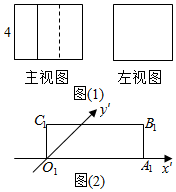 某几何体的主视图和左视图如图(1),它的俯视图的直观图是矩形O1A1B1C1如图(2),其中O1A1=6,O1C1=2,则该几何体的侧面积为( )
某几何体的主视图和左视图如图(1),它的俯视图的直观图是矩形O1A1B1C1如图(2),其中O1A1=6,O1C1=2,则该几何体的侧面积为( )