题目内容
16．已知正数a，b满足2ab+b2=b+1，则a+5b的最小值为$\frac{7}{2}$．分析 正数a，b满足2ab+b2=b+1，可得：a=$\frac{1+b-{b}^{2}}{2b}$＞0．则a+5b=$\frac{1+b-{b}^{2}}{2b}$+5b=$\frac{1}{2}（9b+\frac{1}{b}）$+$\frac{1}{2}$，利用基本不等式的性质即可得出．
解答 解：∵正数a，b满足2ab+b2=b+1，
∴a=$\frac{1+b-{b}^{2}}{2b}$＞0．
则a+5b=$\frac{1+b-{b}^{2}}{2b}$+5b=$\frac{1}{2}（9b+\frac{1}{b}）$+$\frac{1}{2}$≥$\frac{1}{2}×2\sqrt{9b×\frac{1}{b}}$+$\frac{1}{2}$=$\frac{7}{2}$，当且仅当b=$\frac{1}{3}$，a=2时取等号．
故答案为：$\frac{7}{2}$．
点评 本题考查了基本不等式的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
7．已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表：
若抽取学生n人，成绩分为A（优秀）、B（良好）、C（及格）三个等级，设x，y分别表示数学成绩与地理成绩，例如：表中地理成绩为A等级的共有14+40+10=64人，数学成绩为B等级且地理成绩为C等级的有8人．已知x与y均为A等级的概率是0.07．
（1）设在该样本中，数学成绩优秀率是30%，求a，b的值；
（2）已知a≥8，b≥6，求数学成绩为A等级的人数比C等级的人数多的概率．
X 人数 Y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
（1）设在该样本中，数学成绩优秀率是30%，求a，b的值；
（2）已知a≥8，b≥6，求数学成绩为A等级的人数比C等级的人数多的概率．
1．设x∈[0，3]，执行如图所示的程序框图，从输出的结果中随机取一个数a，“2a-10≥0”的概率为（ ）
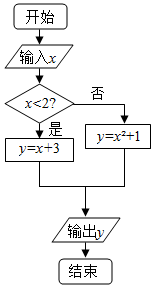
| A． | $\frac{2}{3}$ | B． | $\frac{5}{6}$ | C． | $\frac{5}{7}$ | D． | $\frac{4}{7}$ |
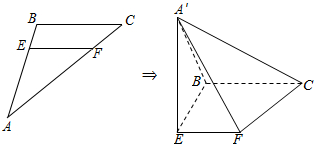已知Rt△ABC中，AB=3，BC=4，∠ABC=90°，AE=2EB，AF=2FC，将△AEF沿EF折起，使A变到A′，使平面A′EF⊥平面EFCB．