题目内容
“a>1”是“函数f(x)=x3+a在R上为单调递增函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:分别由a>1,得到f(x)是增函数,而f(x)是增函数,得不出a>1,从而得到答案.
解答:
解:若a>1,则f′(x)=3x2+a>0,
∴f(x)在R上是增函数,是充分条件,
若函数f(x)=x3+a在R上为单调递增函数,
∴f′(x)=3x2+a>0,
∴a≥0,不是必要条件,
故选:A.
∴f(x)在R上是增函数,是充分条件,
若函数f(x)=x3+a在R上为单调递增函数,
∴f′(x)=3x2+a>0,
∴a≥0,不是必要条件,
故选:A.
点评:本题考查了充分必要条件,考查了函数的单调性,是一道基础题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
已知函数y=2x,g(x)=f(x-2)-1,若g(a)<1<f(a),则实数a的取值范围为( )
| A、(-∞,0)∪(3,+∞) |
| B、(-∞,0) |
| C、(0,3) |
| D、(0,+∞) |
设偶函数f(x)=loga|x+b|在(0,+∞)上是单调的,则f(b-2)与f(a+1)的大小关系为( )
| A、f(b-2)=f(a+1) |
| B、f(b-2)>f(a-1) |
| C、f(b-2)<f(a+1) |
| D、不能确定 |
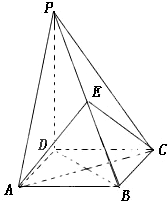 如图,四棱锥P--ABCD的底面是正方形,PD⊥底面ABCD,点E为PB的中点.且PD=
如图,四棱锥P--ABCD的底面是正方形,PD⊥底面ABCD,点E为PB的中点.且PD= 如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.
如图,正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,D是BC的中点.