题目内容
在△ABC中，角A、B、C所对的边分别为a，b，c，且
=
，
（Ⅰ）求cosB；
（Ⅱ）已知b=2
，S△ABC=
，求边长a，c．
| cosC |
| cosB |
| 3a-c |
| b |
（Ⅰ）求cosB；
（Ⅱ）已知b=2
| 2 |
| 2 |
考点：正弦定理
专题：解三角形
分析：（1）根据正弦定理把已知等式中的边转化为角的正弦，整理课求得cosB的值．
（2）利用cosB可求得sinB，根据三角形的面积求得ac的值，进而根据余弦定理求得a和c的关系，联立方程可求得a和c．
（2）利用cosB可求得sinB，根据三角形的面积求得ac的值，进而根据余弦定理求得a和c的关系，联立方程可求得a和c．
解答：
解：（1）由正弦定理知
=
=
，
∴sinBcosC=3sinAcosB-sinCcosB，即sinBcosC+sinCcosB=3sinAcosB，
∴sin（B+C）=sinA=3sinAcosB，
∵sinA≠0，
∴cosB=
．
（2）sinB=
=
，
S△ABC=
acsinB=
ac=
，
∴ac=3，①
cosB=
=
=
，
∴a2+c2=10，②
①②联立求得c=1，a=3，或c=3，a=1．
| cosC |
| cosB |
| 3a-c |
| b |
| 3sinA-sinC |
| sinB |
∴sinBcosC=3sinAcosB-sinCcosB，即sinBcosC+sinCcosB=3sinAcosB，
∴sin（B+C）=sinA=3sinAcosB，
∵sinA≠0，
∴cosB=
| 1 |
| 3 |
（2）sinB=
1-
|
2
| ||
| 3 |
S△ABC=
| 1 |
| 2 |
| ||
| 3 |
| 2 |
∴ac=3，①
cosB=
| a2+c2-b2 |
| 2ac |
| a2+b2-8 |
| 6 |
| 1 |
| 3 |
∴a2+c2=10，②
①②联立求得c=1，a=3，或c=3，a=1．
点评：本题主要考查了正弦定理和余弦定理的应用．解题的关键是利用正弦定理高完成边角问题的转化．
练习册系列答案
小学教材完全解读系列答案
相关题目
设k∈R，则“k≠1”是“直线l：y=kx+
与圆x2+y2=1不相切”的（ ）
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
如图，AE⊥平面DEC，四边形ABCD为正方形，M，N分别是线段BE、DE中点．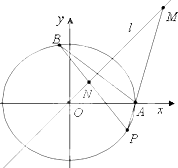
已知A（2，0），B（x0，y0）是椭圆C：
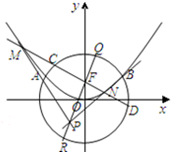已知抛物线x2=2py（p＞0）与圆O：x2+y2=4相交于A、B两点，F为抛物线的焦点，且满足