题目内容
函数f（x）=x（1-x2）在[0，1]上的最大值为 ．
考点：利用导数求闭区间上函数的最值
专题：导数的综合应用
分析：利用导数的性质求解．
解答：
解：∵f（x）=x（1-x2）=x-x3，
∴f′（x）=1-3x2，
由f′（x）=0，得x=
，或x=-
（舍去），
∵f（0）=0，f（
）=
(1-
)=
，f（1）=0，
∴f（x）=x（1-x2）在[0，1]上的最大值为
．
故答案为：
．
∴f′（x）=1-3x2，
由f′（x）=0，得x=
| ||
| 3 |
| ||
| 3 |
∵f（0）=0，f（
| ||
| 3 |
| ||
| 3 |
| 1 |
| 3 |
2
| ||
| 9 |
∴f（x）=x（1-x2）在[0，1]上的最大值为
2
| ||
| 9 |
故答案为：
2
| ||
| 9 |
点评：本题考查函数在闭区间上的最大值的求法，是基础题，解题时要认真审题，注意导数性质的灵活运用．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
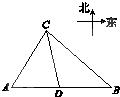如图，港口A北偏东30°方向的C处有一检查站，港口正东方向的B处有一轮船，距离检查站7海里，该轮船从B处沿正西方向航行3海里后到达D处观测站，已知观测站与检查站距离5海里，则此时轮船离港口A有