题目内容
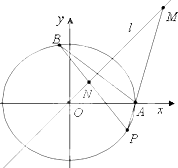 已知A(2,0),B(x0,y0)是椭圆C:
已知A(2,0),B(x0,y0)是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C上异于A,B的动点,若直线AP交M于点M,直线交l于点,试探究
| OM |
| ON |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题意知a=2,设AB:y=-
(x-2),代入
+
=1,得(4b2+9)x2-36x+4(9-4b2)=0,由此利用韦达定理求出AB中点为(
,
),从而能求出椭圆方程.
(Ⅱ)由(Ⅰ)得B(-
,
),设P(x′,y′),M(x1,y1),N(x2,y2),直线AP:y=
(x-2),代入y=x,得x1=
,直线BP:y-
=
(x+
),代入y=x,得x2=
,由此能求出
•
为定值
.
| 3 |
| 4 |
| x2 |
| 4 |
| y2 |
| b2 |
| 18 |
| 4b2+9 |
| 6b2 |
| 4b2+9 |
(Ⅱ)由(Ⅰ)得B(-
| 2 |
| 7 |
| 12 |
| 7 |
| y′ |
| x′-2 |
| -2y′ |
| x′-y′-2 |
| 12 |
| 7 |
y′-
| ||
x′+
|
| 2 |
| 7 |
| ||||
| x′-y′+2 |
| OM |
| ON |
| 24 |
| 7 |
解答:
解:(Ⅰ)∵A(2,0),B(x0,y0)是椭圆C:
+
=1(a>b>0)上两点,
∴a=2,设AB:y=-
(x-2),代入
+
=1,
得(4b2+9)x2-36x+4(9-4b2)=0,
由韦达定理x0+2=
,推导出x0=
,y0=
,
得到AB中点为(
,
),
由
=
,解得b2=3,
∴椭圆方程为
+
=1.
(Ⅱ)由(Ⅰ)得B(-
,
),
设P(x′,y′),M(x1,y1),N(x2,y2),
直线AP:y=
(x-2),代入y=x,得x1=
,
直线BP:y-
=
(x+
),代入y=x,得x2=
,
则
•
=2x1y1=-
•
=
-
•
=-
•
=
.
∴
•
为定值
.
| x2 |
| a2 |
| y2 |
| b2 |
∴a=2,设AB:y=-
| 3 |
| 4 |
| x2 |
| 4 |
| y2 |
| b2 |
得(4b2+9)x2-36x+4(9-4b2)=0,
由韦达定理x0+2=
| 36 |
| 4b2+9 |
| 18-8b2 |
| 4b2+9 |
| 12b2 |
| 4b2+9 |
得到AB中点为(
| 18 |
| 4b2+9 |
| 6b2 |
| 4b2+9 |

由
| 18 |
| 4b2+9 |
| 6b2 |
| 4b2+9 |
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)由(Ⅰ)得B(-
| 2 |
| 7 |
| 12 |
| 7 |
设P(x′,y′),M(x1,y1),N(x2,y2),
直线AP:y=
| y′ |
| x′-2 |
| -2y′ |
| x′-y′-2 |
直线BP:y-
| 12 |
| 7 |
y′-
| ||
x′+
|
| 2 |
| 7 |
| ||||
| x′-y′+2 |
则
| OM |
| ON |
| 8 |
| 7 |
| y′(6x′+y′) |
| (x′-y′)2-4 |
-
| 8 |
| 7 |
| 6x′y′+(y′)2 |
| (x′)2-2x′y′+(y′)2-4 |
=-
| 8 |
| 7 |
| 6x′y′+(y′)2 | ||
4-
|
| 24 |
| 7 |
∴
| OM |
| ON |
| 24 |
| 7 |
点评:本题考查椭圆方程的求法,考查向量的数量积是否为定值的判断,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知数列{an}为等差数列,a1=1,公差d≠0,a1、a2、a5成等比,则a2014的值为( )
| A、4023 | B、4025 |
| C、4027 | D、4029 |
 如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=
如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=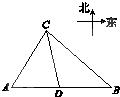 如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站7海里,该轮船从B处沿正西方向航行3海里后到达D处观测站,已知观测站与检查站距离5海里,则此时轮船离港口A有
如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站7海里,该轮船从B处沿正西方向航行3海里后到达D处观测站,已知观测站与检查站距离5海里,则此时轮船离港口A有