题目内容
已知数列{an}满足an+1-3an-1=0(n∈N*)
(Ⅰ)若存在一个常数λ,使得数列{an+λ}为等比数列,求出λ的值;
(Ⅱ)设a1=
,数列{an}的前n和为Sn,求满足Sn>1090的n的最小值.
(Ⅰ)若存在一个常数λ,使得数列{an+λ}为等比数列,求出λ的值;
(Ⅱ)设a1=
| 1 |
| 2 |
考点:数列递推式,等比数列的前n项和
专题:等差数列与等比数列
分析:(Ⅰ)根据等比数列的定义,建立条件关系即可求出λ的值;
(Ⅱ)求出数列{an}的前n和为Sn,解不等式即可得到结论.
(Ⅱ)求出数列{an}的前n和为Sn,解不等式即可得到结论.
解答:
解:(Ⅰ)∵an+1-3an-1=0,即an+1=3an+1
∴设an+1+λ=3(an+λ),
即an+1=3an+2λ,由2λ=1,
解得λ=
,此时数列{an+λ}为等比数列,公比q=3.
(Ⅱ)由(Ⅰ)得an+1+
=3(an+
),
则{an+
}是公比q=3的等比数列,首项a1+
=
+
=1,
则an+
=3n-1则an==3n-1-
.
则Sn=
-
n=
(3n-1-1)-
n,
由Sn>1090得3n-n>2181,
∵S7=2180<2181,S8=6553>2181,
满足Sn>1090的n的最小值为8.
∴设an+1+λ=3(an+λ),
即an+1=3an+2λ,由2λ=1,
解得λ=
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)得an+1+
| 1 |
| 2 |
| 1 |
| 2 |
则{an+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则an+
| 1 |
| 2 |
| 1 |
| 2 |
则Sn=
| 1-3n-1 |
| 1-3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由Sn>1090得3n-n>2181,
∵S7=2180<2181,S8=6553>2181,
满足Sn>1090的n的最小值为8.
点评:本题主要考查等比数列的判断,以及数列的求和,利用等比数列的通项公式和求和公式是解决本题的关键,考查学生的运算能力.

练习册系列答案
相关题目
 如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=
如图,四棱锥P-ABCD,PA⊥底面ABCD,AB∥CD,AB⊥AD,AB=AD=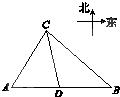 如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站7海里,该轮船从B处沿正西方向航行3海里后到达D处观测站,已知观测站与检查站距离5海里,则此时轮船离港口A有
如图,港口A北偏东30°方向的C处有一检查站,港口正东方向的B处有一轮船,距离检查站7海里,该轮船从B处沿正西方向航行3海里后到达D处观测站,已知观测站与检查站距离5海里,则此时轮船离港口A有