题目内容
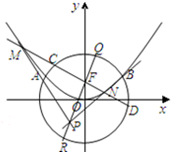 已知抛物线x2=2py(p>0)与圆O:x2+y2=4相交于A、B两点,F为抛物线的焦点,且满足
已知抛物线x2=2py(p>0)与圆O:x2+y2=4相交于A、B两点,F为抛物线的焦点,且满足| OA |
| OB |
| OF |
| OA |
| OB |
(Ⅰ)求抛物线的方程;
(Ⅱ)过点P(t,-1)作抛物线的两条切线,切点分别为M,N,直线MN与圆O交于C,D两点,直线PF与圆O交于Q,R两点,如图所示,四边形CRDQ的面积的取值范围.
考点:圆与圆锥曲线的综合,抛物线的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)确定F为AB的中点,利用
•
=-2,求出∠AOB=
,即可求抛物线的方程;
(Ⅱ)求出切线PM、PN的方程,可得P的坐标,证明MN⊥PF,求出|CD|,|RQ|,即可求得四边形CRDQ的面积的取值范围.
| OA |
| OB |
| 2π |
| 3 |
(Ⅱ)求出切线PM、PN的方程,可得P的坐标,证明MN⊥PF,求出|CD|,|RQ|,即可求得四边形CRDQ的面积的取值范围.
解答:
解:(Ⅰ)x2=2py的焦点F(0,
).
∵
+
=2
,
∴F为AB的中点,
∵
•
=-2,
∴2•2•cos∠AOB=-2,
∴cos∠AOB=-
,
∴∠AOB=
,
在△AOB中,|OF|=
|OB|=1,∴
=1,
∴p=2,
∴抛物线的方程为x2=4y;
(Ⅱ)设M(x1,y1)、N(x2,y2),则
切线PM:y-
=
x1(x-x1),即y=
x1x-
,
同理切线PN:y=
x2x-
,
联立求得P(
,
),则x1+x2=2t,x1x2=-4,
∴直线MN的方程为y=
x-
,即y=
tx+1,
直线PF:y-1=-
(x-6),即y=-
x+1,
∵
t•(-
)=-1,
∴MN⊥PF
O到MN的距离d1=
,∴|CD|=2
=2
;
O到PF的距离d2=
,∴|RQ|=2
=2
,
∴S=
|RQ||CD|=2
•
,
令
=m(m∈(0,1]),则S=2
,
∵(4-m)(3+m)=-(m-
)2+
,
∴(4-m)(3+m)∈[12,
],
∴S∈[4
,7].
| p |
| 2 |
∵
| OA |
| OB |
| OF |
∴F为AB的中点,
∵
| OA |
| OB |
∴2•2•cos∠AOB=-2,
∴cos∠AOB=-
| 1 |
| 2 |
∴∠AOB=
| 2π |
| 3 |
在△AOB中,|OF|=
| 1 |
| 2 |
| p |
| 2 |
∴p=2,
∴抛物线的方程为x2=4y;
(Ⅱ)设M(x1,y1)、N(x2,y2),则
切线PM:y-
| x12 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| x12 |
| 4 |
同理切线PN:y=
| 1 |
| 2 |
| x22 |
| 4 |
联立求得P(
| x1+x2 |
| 2 |
| x1x2 |
| 4 |
∴直线MN的方程为y=
| x1+x2 |
| 4 |
| x1x2 |
| 4 |
| 1 |
| 2 |
直线PF:y-1=-
| 2 |
| t |
| 2 |
| t |
∵
| 1 |
| 2 |
| 2 |
| t |
∴MN⊥PF
O到MN的距离d1=
| 1 | ||||
|
| 4-d12 |
4-
|
O到PF的距离d2=
| 1 | ||||
|
| 4-d22 |
4-
|
∴S=
| 1 |
| 2 |
4-
|
3+
|
令
| 4 |
| t2+4 |
| (4-m)(3+m) |
∵(4-m)(3+m)=-(m-
| 1 |
| 2 |
| 49 |
| 4 |
∴(4-m)(3+m)∈[12,
| 49 |
| 4 |
∴S∈[4
| 3 |
点评:本题考查抛物线的方程,考查圆与圆锥曲线的综合,考查向量知识的运用,考查学生分析解决问题的能力,有难度.

练习册系列答案
相关题目
已知f(x)=xlnx,g(x)=-x2+ax-1,对一切x∈(0,+∞),3f(x)≥g(x)恒成立,则实数a的取值范围是( )
A、(-∞,
| ||||||
| B、(-∞,4] | ||||||
| C、(-∞,6] | ||||||
| D、[5,+∞) |