题目内容
函数y=lgsin(
-
x)的单调减区间是 .
| π |
| 4 |
| 1 |
| 2 |
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:利用函数性质得出即
+2kπ≤
-
x<π+2kπ,k∈z,求解即可.
| π |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
解答:
解:∵函数y=lgsin(
-
x),
∴sin(
-
x)>0,
+2kπ≤
-
x≤
+2kπ,k∈z,
即
+2kπ≤
-
x<π+2kπ,k∈z,
解得:-
+4kπ<x≤-
+4kπ,k∈z,
故答案为:(-
+4kπ,
+4kπ],k∈z
| π |
| 4 |
| 1 |
| 2 |
∴sin(
| π |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| 3π |
| 2 |
即
| π |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
解得:-
| 3π |
| 2 |
| π |
| 2 |
故答案为:(-
| 3π |
| 2 |
| π |
| 2 |
点评:本题考查了复合函数单调定义域,单调性的求解属于中档题,关键确定不等式即可.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
如图所示,在平行六面体ABCD-A1B1C1D1中,点E为上底面对角线A1C1的中点,若
=
+x
+y
,则( )
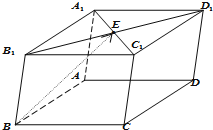
| BE |
| AA1 |
| AB |
| AD |

A、x=-
| ||||
B、x=
| ||||
C、x=-
| ||||
D、x=
|
已知函数y=f(x)是偶函数,且y=f(x)在[0,2]上是减函数,则( )
| A、f(2)<f(-1)<f(0) |
| B、f(-1)<f(0)<f(2) |
| C、f(-1)<f(2)<f(0) |
| D、f(0)<f(-1)<f(2) |
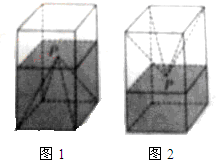 如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P,如果将容器倒置,水面也恰好过点P(如图2),有下列三个命题:
如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P,如果将容器倒置,水面也恰好过点P(如图2),有下列三个命题: