题目内容
若在直角坐标平面内A,B两点满足条件:
①点A,B都在函数y=f(x)的图象上;
②点A,B关于原点对称,则称A,B为函数y=f(x)的一个“黄金点对”.
那么函数f(x)=
的“黄金点对”的个数是( )
①点A,B都在函数y=f(x)的图象上;
②点A,B关于原点对称,则称A,B为函数y=f(x)的一个“黄金点对”.
那么函数f(x)=
|
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:分段函数的应用
专题:数形结合,函数的性质及应用
分析:根据题意:由“黄金点对”,可知,欲求f(x)的“黄金点对”,只须作出函数y=x2+2x-2(x≤0)的图象关于原点对称的图象,看它与函数y=
(x>0)交点个数即可.
| 1 | ||
|
解答:
 解:根据题意:由“黄金点对”,可知,
解:根据题意:由“黄金点对”,可知,
欲求f(x)的“黄金点对”,
只须作出函数y=x2+2x-2(x≤0)
的图象关于原点对称的图象,
看它与函数y=
(x>0)交点个数即可.
如图,
观察图象可得:它们的交点个数是:2.
即f(x)的“黄金点对”有:2个.
故选:C.
 解:根据题意:由“黄金点对”,可知,
解:根据题意:由“黄金点对”,可知,欲求f(x)的“黄金点对”,
只须作出函数y=x2+2x-2(x≤0)
的图象关于原点对称的图象,
看它与函数y=
| 1 | ||
|
如图,
观察图象可得:它们的交点个数是:2.
即f(x)的“黄金点对”有:2个.
故选:C.
点评:本题主要考查了奇偶函数图象的对称性,以及数形结合的思想,解答的关键在于对“黄金点对”的正确理解,合理地利用图象法解决.

练习册系列答案
相关题目
函数f(x)=
+
的定义域是( )
| x-1 |
| 1 |
| x-2 |
| A、[1,+∞) |
| B、(2,+∞) |
| C、(1,2) |
| D、[1,2)∪(2,+∞) |
方程x
-(
)x-2=0的解所在的区间为( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
棱锥侧面是有公共顶点的三角形,若围成一个棱锥侧面的三角形都是正三角形,则这样侧面的个数最多有几个( )
| A、3 | B、4 | C、5 | D、6 |
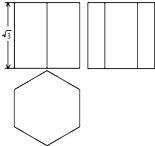 如图是一个六棱柱的三视图,俯视图是一个周长为3的正六边形,该六棱柱的顶点都在同一个球面上,那么这个球的体积为( )
如图是一个六棱柱的三视图,俯视图是一个周长为3的正六边形,该六棱柱的顶点都在同一个球面上,那么这个球的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=
的定义域是( )
| ||
| lgx-1 |
| A、[4,+∞) |
| B、(10,+∞) |
| C、(4,10)∪(10,+∞) |
| D、[4,10)∪(10,+∞) |
若a≠b,数列a,x1,x2,b和数列a,y1,y2,y3,b都是等差数列,则
=( )
| x2-x1 |
| y2-y1 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|