题目内容
若⊙O1与⊙O2相切,且O1O2=5,⊙O1的半径r1=2,则⊙O2的半径r2是( )
| A、3 | B、5 | C、7 | D、3或7 |
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:两圆相切,包括了内切或外切,即d=R+r,d=R-r,分别求解.
解答:
解:∵这两圆相切
∴⊙O1与⊙O2的位置关系是内切或外切,
O1O2=5,⊙O1的半径r1=2,
所以外切:r1+r2=5解得r2=3或内切:r2-r1=5,解得r2=7.
故选:D.
∴⊙O1与⊙O2的位置关系是内切或外切,
O1O2=5,⊙O1的半径r1=2,
所以外切:r1+r2=5解得r2=3或内切:r2-r1=5,解得r2=7.
故选:D.
点评:本题考查了由两圆位置关系来判断半径和圆心距之间数量关系的方法.两圆的半径分别为R和r,且R≥r,圆心距为d:外离d>R+r;外切d=R+r;相交R-r<d<R+r;内切d=R-r;内含d<R-r.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
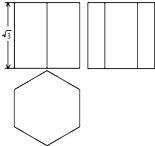 如图是一个六棱柱的三视图,俯视图是一个周长为3的正六边形,该六棱柱的顶点都在同一个球面上,那么这个球的体积为( )
如图是一个六棱柱的三视图,俯视图是一个周长为3的正六边形,该六棱柱的顶点都在同一个球面上,那么这个球的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
某储蓄所计划从2011年起,力争做到每年的吸储量比前一年增长8%,则到2014年底该储蓄所的吸储量将比2011年的吸储量增加( )
| A、24% |
| B、32% |
| C、(1.083-1)×100% |
| D、(1.084-1)×1.083 |
若a≠b,数列a,x1,x2,b和数列a,y1,y2,y3,b都是等差数列,则
=( )
| x2-x1 |
| y2-y1 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
设G是△ABC的重心,且sinA
+sinB
+sinC
=
,则∠B的值为( )
| GA |
| GB |
| GC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
,若f(a)=4,则实数a=( )
|
| A、-2或6 | ||
B、-2或
| ||
| C、-2或2 | ||
D、2或
|