题目内容
已知tanα=-
，则
的值为（ ）
| 1 |
| 2 |
| (sinα-cosα)2 |
| cos2α |
| A、2 | B、-2 | C、3 | D、-3 |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：原式利用同角三角函数间的基本关系变形后，将tanα的值代入计算即可求出值．
解答：
解：∵tanα=-
，
∴原式=
=
=
=3．
故选：C．
| 1 |
| 2 |
∴原式=
| sin2α+cos2α-2sinαcosα |
| cos2α-sin2α |
| tan2α+1-2tanα |
| 1-tan2α |
| ||
1-
|
故选：C．
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设函数f（x）=x2-5x+6，x∈[0，5]，若从区间[0，5]内随机选取一个实数x0，则所选取的实数x0满足f（x0）≤0的概率为（ ）
| A、0.2 | B、0.3 |
| C、0.4 | D、0.5 |
集合A={x∈R|ax2+ax+1=0}的子集只有2个，则a=（ ）
| A、4 | B、2 | C、0 | D、0或4 |
下列结论正确的是（ ）
| A、若x≥10，则x＞10 |
| B、若x2＞25，则x＞5 |
| C、若x＞y，则x2＞y2 |
| D、若x2＞y2，则|x|＞|y| |
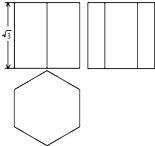如图是一个六棱柱的三视图，俯视图是一个周长为3的正六边形，该六棱柱的顶点都在同一个球面上，那么这个球的体积为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
等比数列{an}中，a4=5，则a3a5的值（ ）
| A、75 | B、50 | C、25 | D、10 |
某储蓄所计划从2011年起，力争做到每年的吸储量比前一年增长8%，则到2014年底该储蓄所的吸储量将比2011年的吸储量增加（ ）
| A、24% |
| B、32% |
| C、（1.083-1）×100% |
| D、（1.084-1）×1.083 |
设G是△ABC的重心，且sinA
+sinB
+sinC
=
，则∠B的值为（ ）
| GA |
| GB |
| GC |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|