题目内容
已知函数f(x)=
x2-ax+(a-1)lnx,求函数f(x)的极值.
| 1 |
| 2 |
考点:利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:求导数,分类讨论,利用极值的定义求解即可.
解答:
解:∵f(x)=
x2-ax+(a-1)lnx,
∴f′(x)=
,
a=2时,f′(x)≥0,函数无极值;
a>2时,(0,1)上函数单调递增,(1,a-1)上函数单调递减,(a-1,+∞)上函数单调递增,
∴x=1时,函数取得极大值
-a;x=a-1时,函数取得极小值
(a-1)(a-2)+(a-1)ln(a-1);
1<a<2时,(0,a-1)上函数单调递增,(a-1,1)上函数单调递减,(1,+∞)上函数单调递增,
∴x=a-1时,函数取得极大值
(a-1)(a-2)+(a-1)ln(a-1);x=1时,函数取得极小值
-a;
a≤1时,(0,1)上函数单调递减,(1,+∞)上函数单调递增,
∴x=1时,函数取得极小值
-a,无极大值.
| 1 |
| 2 |
∴f′(x)=
| (x-1)[x-(a-1)] |
| x |
a=2时,f′(x)≥0,函数无极值;
a>2时,(0,1)上函数单调递增,(1,a-1)上函数单调递减,(a-1,+∞)上函数单调递增,
∴x=1时,函数取得极大值
| 1 |
| 2 |
| 1 |
| 2 |
1<a<2时,(0,a-1)上函数单调递增,(a-1,1)上函数单调递减,(1,+∞)上函数单调递增,
∴x=a-1时,函数取得极大值
| 1 |
| 2 |
| 1 |
| 2 |
a≤1时,(0,1)上函数单调递减,(1,+∞)上函数单调递增,
∴x=1时,函数取得极小值
| 1 |
| 2 |
点评:本题考查利用导数研究函数的极值,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
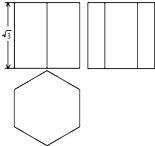 如图是一个六棱柱的三视图,俯视图是一个周长为3的正六边形,该六棱柱的顶点都在同一个球面上,那么这个球的体积为( )
如图是一个六棱柱的三视图,俯视图是一个周长为3的正六边形,该六棱柱的顶点都在同一个球面上,那么这个球的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
,若f(a)=4,则实数a=( )
|
| A、-2或6 | ||
B、-2或
| ||
| C、-2或2 | ||
D、2或
|