题目内容
7.记函数f(x)=lg(x2-1)的定义域为A,g(x)=$\sqrt{(x-a-1)(2a-x)}$(其中a<1)的定义域为B.(1)求A;
(2)若B⊆A,求实数a的取值范围.
分析 (1)根据函数f(x)的解析式,对数的真数大于0,列出不等式即可求出f(x)的定义域;
(2)根据g(x)的解析式,二次根式的被开方数大于或等于0,列出不等式求出g(x)的定义域,再根据B⊆A,求出a的取值范围.
解答 解:(1)∵函数f(x)=lg(x2-1),
∴x2-1>0,
解得x<-1或x>1;
∴f(x)的定义域为A={x|x<-1或x>1};
(2)∵g(x)=$\sqrt{(x-a-1)(2a-x)}$(其中a<1),
∴(x-a-1)(2a-x)≥0,
即(x-a-1)(x-2a)≤0,
解得2a≤x≤a+1,
∴g(x)的定义域为B={x|2a≤x≤a+1};
又B⊆A,当2a≥a+1时,即a≥1,不合题意,舍去;
当a<1时,有a+1<-1或2a>1,
解得a<-2或a>$\frac{1}{2}$,
所以实数a的取值范围是{a|a<-2或$\frac{1}{2}$<a<1}.
点评 本题考查了根据函数的解析式求定义域的应用问题,也考查了集合的运算问题,是综合性题目.

练习册系列答案
相关题目
17.设复数z满足(2-i)z=5i(i为虚数单位),则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.已知x≥0,y≥0,x2+y2=4,μ=x•y-4(x+y)+10,μ的最值情况是( )
| A. | 有最大值2,最小值2(2-$\sqrt{2}$)2 | B. | 有最大值2,最小值0 | ||
| C. | 有最大值10,最小值2(2-$\sqrt{2}$)2 | D. | 最值不存在 |
12.如表是关于出生男婴与女婴调查的列联表,那么A=53,B=35,C=100,D=82.
| 晚上 | 白天 | 总计 | |
| 男婴 | 45 | B | |
| 女婴 | A | 47 | C |
| 总计 | 98 | D | 180 |
 棱长为1的正方形ABCD-A1B1C1D1中,给出以下结论:
棱长为1的正方形ABCD-A1B1C1D1中,给出以下结论: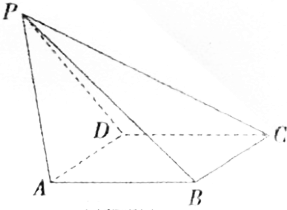 如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BDA=60°.
如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BDA=60°.